A glass cube of edge $1$$cm$and having a refractive index $n = 1.5$ has a small spot at the centre. What parts of the cube face must be covered to prevent the spot from being seen, no matter what the direction of viewing?
(A) With a circular path of radius $0.45$$cm$
(B) With a square of side $1$$cm$
(C) It cannot be covered
(D) None of the above
Verified119.7k+ views
Hint:To solve this question, consider the cone of vision. The cone of vision is an imaginary cone that contains the rays of light that will enter the eyes in order for the object to be visible. Consider the circle that will form at the face of the cube, the area of that circle must be considered. Only the rays that are inside the cone will be visible.
Complete step by step solution:
Consider the light coming from the spot. There will be a circle of radius $r$ outside which the light will not come out. Consider the side view of the cube. The light hit the inner face of the cube and will get refracted. If the light after refraction travels in a direction which is perpendicular to the normal at the point of refraction, the object will never be seen. The above consideration is depicted below:
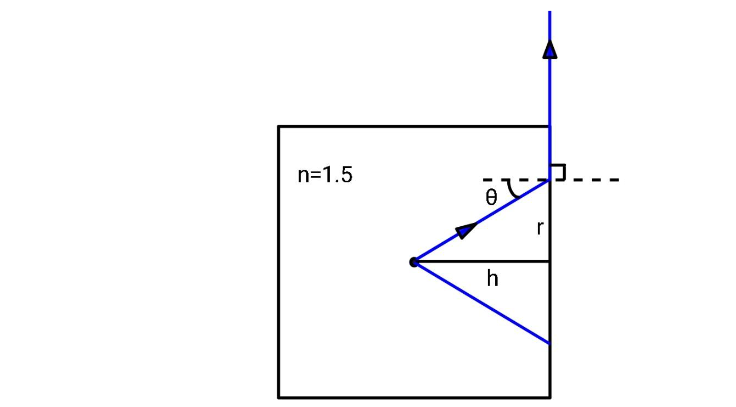
Applying Snell’s Law at the point of refraction,
${n_1}\sin {\theta _1} = {n_2}\sin {\theta _2}$. In our case, ${n_1} = n = 1.5$, ${n_2} = 1$, ${\theta
_1} = \theta $ and ${\theta _2} = \dfrac{\pi }{2}$. Substituting these values in the above equation,
we get,
$
n\sin \theta = \left( 1 \right)\sin \dfrac{\pi }{2} \\
n\sin \theta = 1 \\
$
From the above figure, you can see that $\sin \theta = \dfrac{r}{{\sqrt {{r^2} + {h^2}} }}$
Therefore,
$
\dfrac{{nr}}{{\sqrt {{r^2} + {h^2}} }} = 1 \\
{n^2}{r^2} = {r^2} + {h^2} \\
\left( {{n^2} - 1} \right){r^2} = {h^2} \\
r = \dfrac{h}{{\sqrt {{n^2} - 1} }} \\
$
Here, $h = 0.5$$cm$
$r = \dfrac{{0.5}}{{\sqrt {{{1.5}^2} - 1} }} = \dfrac{{0.5}}{{\sqrt {2.25 - 1} }} = \dfrac{{0.5}}{{\sqrt
{1.25} }} = 0.447 \approx 0.45$$cm$
Therefore, parts of the cube face that must be covered to prevent the spot from being seen, no matter what the direction of viewing is, will be a circular path of radius $0.45$$cm$.
Thus,the correct option is (A).
Note:To solve these types of questions, always consider the refraction at the interface of the two mediums. To derive the condition which gives relation between the refractive indices of the two medium, the angle of refraction and angle of incidence, consider the Snell’s Law.
Complete step by step solution:
Consider the light coming from the spot. There will be a circle of radius $r$ outside which the light will not come out. Consider the side view of the cube. The light hit the inner face of the cube and will get refracted. If the light after refraction travels in a direction which is perpendicular to the normal at the point of refraction, the object will never be seen. The above consideration is depicted below:
Applying Snell’s Law at the point of refraction,
${n_1}\sin {\theta _1} = {n_2}\sin {\theta _2}$. In our case, ${n_1} = n = 1.5$, ${n_2} = 1$, ${\theta
_1} = \theta $ and ${\theta _2} = \dfrac{\pi }{2}$. Substituting these values in the above equation,
we get,
$
n\sin \theta = \left( 1 \right)\sin \dfrac{\pi }{2} \\
n\sin \theta = 1 \\
$
From the above figure, you can see that $\sin \theta = \dfrac{r}{{\sqrt {{r^2} + {h^2}} }}$
Therefore,
$
\dfrac{{nr}}{{\sqrt {{r^2} + {h^2}} }} = 1 \\
{n^2}{r^2} = {r^2} + {h^2} \\
\left( {{n^2} - 1} \right){r^2} = {h^2} \\
r = \dfrac{h}{{\sqrt {{n^2} - 1} }} \\
$
Here, $h = 0.5$$cm$
$r = \dfrac{{0.5}}{{\sqrt {{{1.5}^2} - 1} }} = \dfrac{{0.5}}{{\sqrt {2.25 - 1} }} = \dfrac{{0.5}}{{\sqrt
{1.25} }} = 0.447 \approx 0.45$$cm$
Therefore, parts of the cube face that must be covered to prevent the spot from being seen, no matter what the direction of viewing is, will be a circular path of radius $0.45$$cm$.
Thus,the correct option is (A).
Note:To solve these types of questions, always consider the refraction at the interface of the two mediums. To derive the condition which gives relation between the refractive indices of the two medium, the angle of refraction and angle of incidence, consider the Snell’s Law.