Question

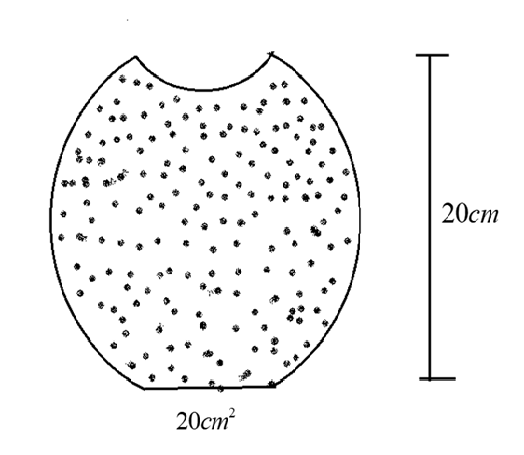
A glass full of water has a bottom of area 20cm2, top of area 20cm2, height 20cm and volume half a liter.
(a) Find the force exerted by the water on the bottom.
(b) Considering the equilibrium of the water, find the resultant force exerted by the sides of the glass on the water. Atmospheric pressure $= 1.0 \times {10^5}N{m^{ - 2}}$, density of water$ = 1000kg{m^{ - 3}}$ and $g = 10m{s^{ - 2}}$. Take all numbers to be exact.

Answer 1

Hint: A fluid always exerts a force on any surface in contact with it. The force so exerted is always normal to that surface. The lesser the area the pressure is high and the area is large the pressure is less.

Complete step by step answer:
Given, A glass full of water has a bottom of area $20 \times {10^{ - 4}}{m^2}$ we have converted the centimeters into meters.
Top of area $20 \times {10^{ - 4}}{m^2}$
Height of the glass beaker\[ = 20cm \Rightarrow 0.2m\]
Atmospheric pressure${P_a} = $ $1.0 \times {10^5}N{m^{ - 2}}$,
Density of water${\rho _w} = 1000kg{m^{ - 3}}$
Acceleration due to gravity $g = 10m{s^{ - 2}}$
Let us consider the given image in the question as a reference. Here in the image the width and the height of the glass filled with the water are given. The width is $20c{m^2}$ and the height is $20cm$.

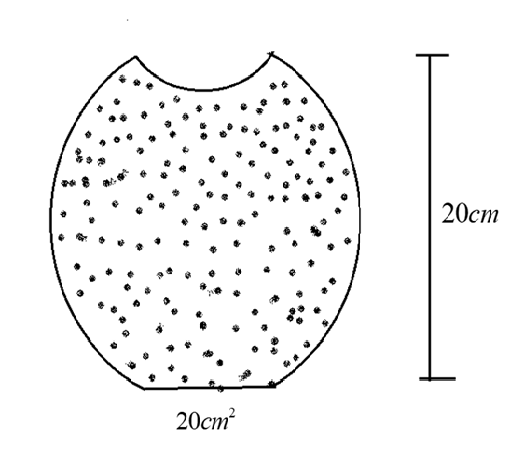
(a) Now let us calculate the force exerted by the water on the bottom.
Total pressure at the bottom = (atmospheric pressure) + (pressure of the liquid)
${P_t} = {P_a} + {\rho _w}gh$
$ \Rightarrow {P_t} = 1.0 \times {10^5} + (1000)(10)(0.2)$
$ \Rightarrow {P_t} = 102000N{m^{ - 2}}$
This is the total amount of pressure acting at the bottom. Now we can find force exerted by the water on the bottom,
We have, ${\text{pressure = }}\dfrac{{{\text{force}}}}{{{\text{area}}}}$
From this, we can write
${\text{force = pressure} \times \text{area}}$
$ \Rightarrow F = 102000 \times 20 \times {10^{ - 4}}$
$ \Rightarrow F = 204N$
Therefore, $240N$ is the force exerted by the water on the bottom.

(b) At equilibrium of the water, let a given glass beaker in spherical form or shape. So, radius of the sphere \[r = 10cm \Rightarrow 0.1m\;\]( half of the height of the glass)
Then average pressure exerted by the liquid along the depth is given by,
${P_{avg}} = \dfrac{{\rho gh}}{2}$
$ \Rightarrow {P_{avg}} = \dfrac{{1000 \times 10 \times 0.2}}{2}$
$ \Rightarrow 1000N{m^{ - 2}}$
Now total pressure=(atmospheric pressure)+(average pressure)
${P_{total}} = {P_a} + {P_{avg}}$
 $ \Rightarrow {P_{total}} = 100000 + 1000$
$ \Rightarrow 101000N{m^{ - 2}}$
Therefore, resultant force exerted by the sides of the glass on the water is,
${\text{force = pressure} \times \text{area}}$
Area of sphere is given by $4\pi {r^2}$
${F_r} = 101000 \times 4\pi {r^2}$
$ \Rightarrow {F_r} = 101000 \times 4 \times 3.14 \times {0.1^2}$
$\therefore 1.26 \times {10^4}N.$

Thus, the resultant force exerted by the sides of the glass on the water is $1.26 \times {10^4}N$.

Additional information:
Earth is surrounded by a gaseous envelope called atmosphere or air. The atmosphere consists of gases like nitrogen and oxygen with traces of carbon dioxide, inert gases, and water vapors. The density of the atmosphere goes on decreasing as one goes above the surface of the earth. Atmospheric pressure is defined as the thrust exerted by the atmosphere per unit area. It is maximum at the surface of the earth and decreases with an increase in height.

Note:
The pressure at a point is defined as the fluid thrust (normal force) per unit area.
If the thrust or upward force is uniform then the pressure at every point of the surface is the same.
A barometer is an instrument that is used to measure the pressure.