Question

A glass slab is placed in a medium of higher refractive index than glass. A light ray incident from one surface exits from the opposite surface. Then,
A. Angle of emergence = Angle of incidence
B. Emergent ray is parallel to incident ray
C. Behavior is similar to glass slab in air
D. All of the above

Answer 1

Hint:When the light ray travels from rarer medium to denser medium, the path of light bends towards the normal. Use Snell’s law at three surfaces where the light ray undergoes refraction. Identify the relation between angle of incidence and angle of refraction.

Complete answer:
From Snell’s law, we know that when the light ray travels from a rarer medium to a denser medium, the path of light bends towards the normal. In this case, since the glass slab has a lower refractive index than the medium that is placed next to it, the light ray will deviate towards the normal. Let’s draw the ray diagram of the situation given in the question as shown in the figure below.

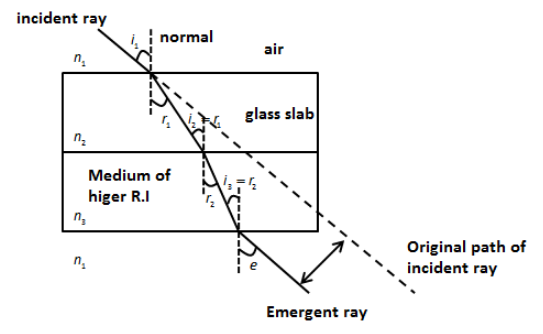
In the above figure, \[{n_1}\] is the refractive index of air, \[{n_2}\] is the refractive index of the glass slab, \[{n_3}\] is the refractive index of the medium.
Now, let’s express Snell’s law for the first surface as follows,
\[{n_1}\sin {i_1} = {n_2}\sin {r_1}\]
But we know that the refractive index of air is 1. Therefore,
\[\sin {i_1} = {n_2}\sin {r_1}\] …… (1)

Let’s express Snell’s law for second surface as follows,
\[{n_2}\sin {i_2} = {n_3}\sin {r_2}\]
But from the geometry of the figure, we have, \[{i_2} = {r_1}\]. Therefore, the above becomes,
\[{n_2}\sin {r_1} = {n_3}\sin {r_2}\] …… (2)

Let’s express Snell’s law for the third surface as follows,
\[{n_3}\sin {i_3} = {n_1}\sin e\]
\[ \Rightarrow {n_3}\sin {i_3} = \sin e\]
Here, e is the angle of emergence.

From the geometry of the above figure, we have, \[{i_3} = {r_2}\]. Therefore, the above equation becomes,
\[{n_3}\sin {r_2} = \sin e\] …… (3)
Using equation (2) in the above equation, we get,
\[{n_2}\sin {r_1} = \sin e\]
Using equation (1) in the above equation, we get,
\[\therefore\sin {i_1} = \sin e\]
Therefore, the angle of incidence equals the angle of emergence. Thus, the option (A) is correct.

Since the angle of incidence is equal to the angle of emergence, we can say that the emergent ray is parallel to the path of the incident ray. Therefore, the option B is also correct.

We know that when the light ray comes out of the glass slab, it laterally shifts with respect to the incident ray. In our case, we can see the lateral displacement of the emergent ray. Thus, the behavior is similar to the glass slab in the air. Therefore, the option C is also correct.

So, the correct answer is option D.

Note: There is not much difference between emergent ray and refracted ray. The emergent ray is the ray that emerges out from the medium after undergoing refraction. The crucial step in this solution is to identify the incidence angle and refraction angle. Always remember, the angle of refraction is equal to angle of incidence when the light ray undergoes two refractions simultaneously.