
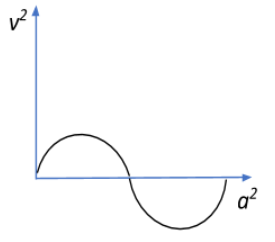
A graph of the square of the velocity against the square of the acceleration of a given simple harmonic motion is:
A.
B.
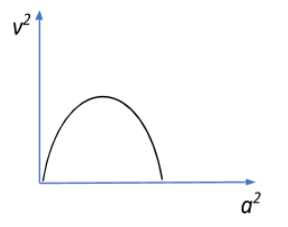
C.
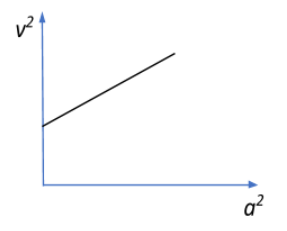
D.
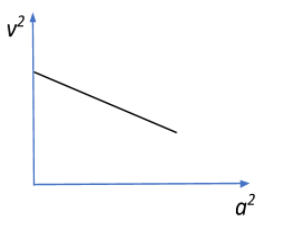




Answer
573.3k+ views
Hint: Begin with the equation for displacement of a particle performing SHM that is in terms of amplitude, phase and frequency. Take the time derivative of this equation to obtain the velocity equation and square it. Then take the time derivative of the velocity equation to obtain the acceleration and square this as well. Combine the two equations and strategically rearrange the terms in such a way that you are able to reproduce an equation for a plane curve that corresponds to the appropriate graph.
Formula Used:
Displacement of an object performing SHM: $x = A\;sin(\omega t)$
Velocity of an object performing SHM: $v = A\omega\;cos(\omega t)$
Acceleration of an object performing SHM: $a = -A\omega^2sin(\omega t)$
Complete answer:
A simple harmonic motion (SHM) is a type of periodic motion where the force acting on the oscillating object is directly proportional to the magnitude of the object’s displacement and is always directed towards the object’s equilibrium position. This is given as:
$\vec{F}_{restoring} \propto -\vec{x}$, where the negative sign indicates that the restoring force is directed towards the oscillating body’s equilibrium position.
For any SHM, the displacement of its vibrating constituent at any instant of time t is given by:
$x = A\;sin(\omega t)$, where A is the amplitude of oscillation (which is the maximum displacement from mean position) and $\omega$ is the angular frequency.
The speed of the SHM oscillations at any instant of time t is given by taking the derivative of the above equation, i.e.,
$v = \dfrac{dx}{dt}=\dfrac{d}{dt} (A\;sin(\omega t)) = A\omega\;cos(\omega t)$
The acceleration of the SHM oscillations is given by taking the derivative of the above equation:
$a = \dfrac{dv}{dt} = \dfrac{d}{dt}( A\omega\;(cos\omega t)) = -A\omega^2sin(\omega t)$
Now, let us square the expressions we got for the velocity and acceleration of SHM oscillations:
$v^2 = A^2\omega^2\;cos^2(\omega t) \Rightarrow \dfrac{v^2}{A^2\omega^2} = cos^2(\omega t)$, and
$a^2 = A^2\omega^4sin^2(\omega t) \Rightarrow \dfrac{a^2}{A^2\omega^4} = sin^2(\omega t)$
Adding the above two equations, we get:
$\dfrac{v^2}{A^2\omega^2} + \dfrac{a^2}{A^2\omega^4} = cos^2(\omega t) + sin^2(\omega t)$
$\Rightarrow \dfrac{v^2}{A^2\omega^2} + \dfrac{a^2}{A^2\omega^4} = 1$
This equation represents an ellipse, whose general equation is:
$\dfrac{y^2}{b^2}+\dfrac{x^2}{a^2}=1$
Here, $x=a,\; y=v,\; a=A\omega^2$ and $b = A\omega$, and a and b are the semi-major and semi-minor axes of the ellipse respectively.
Therefore, the graph closest to this approximation.
So hence the correct option, would be B.
Note:
Remember that for a particle executing SHM, at mean position, the velocity of the particle is maximum and the acceleration of the particle is minimum, whereas at the extreme position, the velocity is minimum and the acceleration of the particle is maximum. This can be used to heuristically determine the shape of the graph between the velocity and acceleration, which ultimately is an ellipse:
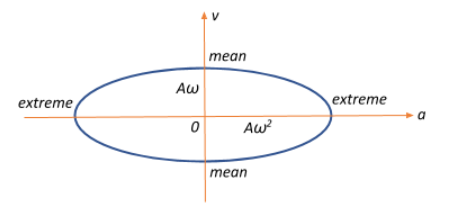
Formula Used:
Displacement of an object performing SHM: $x = A\;sin(\omega t)$
Velocity of an object performing SHM: $v = A\omega\;cos(\omega t)$
Acceleration of an object performing SHM: $a = -A\omega^2sin(\omega t)$
Complete answer:
A simple harmonic motion (SHM) is a type of periodic motion where the force acting on the oscillating object is directly proportional to the magnitude of the object’s displacement and is always directed towards the object’s equilibrium position. This is given as:
$\vec{F}_{restoring} \propto -\vec{x}$, where the negative sign indicates that the restoring force is directed towards the oscillating body’s equilibrium position.
For any SHM, the displacement of its vibrating constituent at any instant of time t is given by:
$x = A\;sin(\omega t)$, where A is the amplitude of oscillation (which is the maximum displacement from mean position) and $\omega$ is the angular frequency.
The speed of the SHM oscillations at any instant of time t is given by taking the derivative of the above equation, i.e.,
$v = \dfrac{dx}{dt}=\dfrac{d}{dt} (A\;sin(\omega t)) = A\omega\;cos(\omega t)$
The acceleration of the SHM oscillations is given by taking the derivative of the above equation:
$a = \dfrac{dv}{dt} = \dfrac{d}{dt}( A\omega\;(cos\omega t)) = -A\omega^2sin(\omega t)$
Now, let us square the expressions we got for the velocity and acceleration of SHM oscillations:
$v^2 = A^2\omega^2\;cos^2(\omega t) \Rightarrow \dfrac{v^2}{A^2\omega^2} = cos^2(\omega t)$, and
$a^2 = A^2\omega^4sin^2(\omega t) \Rightarrow \dfrac{a^2}{A^2\omega^4} = sin^2(\omega t)$
Adding the above two equations, we get:
$\dfrac{v^2}{A^2\omega^2} + \dfrac{a^2}{A^2\omega^4} = cos^2(\omega t) + sin^2(\omega t)$
$\Rightarrow \dfrac{v^2}{A^2\omega^2} + \dfrac{a^2}{A^2\omega^4} = 1$
This equation represents an ellipse, whose general equation is:
$\dfrac{y^2}{b^2}+\dfrac{x^2}{a^2}=1$
Here, $x=a,\; y=v,\; a=A\omega^2$ and $b = A\omega$, and a and b are the semi-major and semi-minor axes of the ellipse respectively.
Therefore, the graph closest to this approximation.
So hence the correct option, would be B.
Note:
Remember that for a particle executing SHM, at mean position, the velocity of the particle is maximum and the acceleration of the particle is minimum, whereas at the extreme position, the velocity is minimum and the acceleration of the particle is maximum. This can be used to heuristically determine the shape of the graph between the velocity and acceleration, which ultimately is an ellipse:

Recently Updated Pages
Master Class 11 Chemistry: Engaging Questions & Answers for Success

Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




