Answer
Verified401.4k+ views
Hint: We first try to explain the concept of squares and rhombus. We also discuss the relation between them. We use that to find the concept of non-square rhombus with help of diagrams.
Complete step-by-step answer:
A parallelogram can be defined in the form of a quadrilateral which has its opposite sides parallel or equal or both. It has no particular condition of consecutive sides being congruent to each other. If the consecutive sides of parallelogram are equal then it becomes a particular form of parallelogram which is rhombus.
Since a square, a rhombus and a rectangle are also parallelograms, they are also excluded.
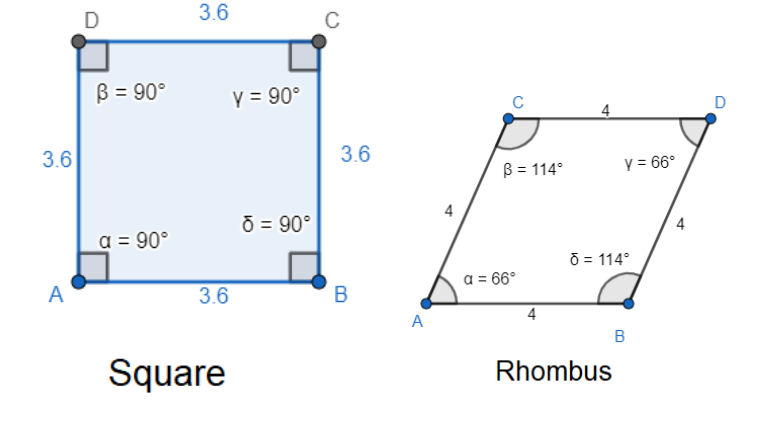
We have also rhombus which have all four sides equal and they have one angle being equal to $ {{90}^{\circ }} $ , then all of the angles become $ {{90}^{\circ }} $ due to the equality of the sides and it becomes square.
Now when we take a square, we can define it in the form of a rhombus where a rhombus converts into a square with its all angles being equal to each other. This means the angles of the square become equal to $ \dfrac{\pi }{2} $ . Therefore, only the square has 4 sides equal and 4 right angles. The correct option is A.
So, the correct answer is “Option A”.
Note: Squares, rectangles and rhombus are all parts of a parallelogram. The main division of parallelograms is where the quadrilateral has equal or parallel opposite sides. Therefore, the specific figure of the square is also part of the rhombus.
Complete step-by-step answer:
A parallelogram can be defined in the form of a quadrilateral which has its opposite sides parallel or equal or both. It has no particular condition of consecutive sides being congruent to each other. If the consecutive sides of parallelogram are equal then it becomes a particular form of parallelogram which is rhombus.
Since a square, a rhombus and a rectangle are also parallelograms, they are also excluded.
We have also rhombus which have all four sides equal and they have one angle being equal to $ {{90}^{\circ }} $ , then all of the angles become $ {{90}^{\circ }} $ due to the equality of the sides and it becomes square.
Now when we take a square, we can define it in the form of a rhombus where a rhombus converts into a square with its all angles being equal to each other. This means the angles of the square become equal to $ \dfrac{\pi }{2} $ . Therefore, only the square has 4 sides equal and 4 right angles. The correct option is A.
So, the correct answer is “Option A”.
Note: Squares, rectangles and rhombus are all parts of a parallelogram. The main division of parallelograms is where the quadrilateral has equal or parallel opposite sides. Therefore, the specific figure of the square is also part of the rhombus.