Question

A heavy bass-sphere is hung from a spiral spring and it executes vertical vibrations with period T. The ball is now immersed in non-viscous liquid with a density one-tenth that of brass. When set into vertical vibrations with the sphere remaining inside the liquid all the time, the period will be-
A. $\left( \dfrac{9}{10} \right)T$
B. $T\sqrt{\left( \dfrac{10}{9} \right)}$
C. unchanged
D.$T\sqrt{\left( \dfrac{9}{10} \right)}$

Answer 1

Hint: Consider all the forces acting on the system before immersion in the non-viscous liquid also after the immersion. Recall the expression for the time period of a spring mass system and also note down the quantities on which the time period depends. Now, see whether any of these quantities got affected due to the system being immersed in the liquid. If yes, find the time period accordingly.

Formula used:
Expression for time period of a spring-mass system,
$T=2\pi \sqrt{\dfrac{m}{k}}$

Complete step by step answer:
We are given a heavy brass sphere hung from a spiral spring which is executing vertical vibrations with period T.

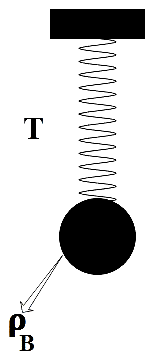
From the Hooke’s law we have the restoring force acting on the spring is directly proportional to the displacement. That is,
$F\propto x$
But F=ma from Newton’s second law.
Let $\dot{x}$ be the first derivative of x (velocity), then, $\ddot{x}$ is the second derivative (acceleration).
$F=m\ddot{x}=-kx$ ……………………….. (1)
Where, k is the proportionality constant called the spring constant. The negative sign here shows that the displacement is in the opposite direction to that of the restoring force.
Now, let us solve the above differential equation. We will get a solution in oscillatory form.
$x=A\cos \left( \dfrac{2\pi t}{T} \right)$ …………………….. (2)
Where, A is the amplitude of oscillation (maximum displacement), t is the total time taken for completing the oscillation and T is the time period of the pendulum.
$\ddot{x}=-{{\left( \dfrac{2\pi }{T} \right)}^{2}}A\cos \left( \dfrac{2\pi t}{T} \right)$ ………………………. (3)
Substituting (2) and (3) in (1), we get,
$-m{{\left( \dfrac{2\pi }{T} \right)}^{2}}A\cos \left( \dfrac{2\pi t}{T} \right)=-kA\cos \left( \dfrac{2\pi t}{T} \right)$
Clearly,
$m{{\left( \dfrac{2\pi }{T} \right)}^{2}}=k$
So, we get the time period for the oscillation of a spring-mass system as,
$T=2\pi \sqrt{\dfrac{m}{k}}$ ……………………………. (4)
Clearly, the time period of the system only depends on the mass and spring constant.
In the given question, this system is further immersed in a viscous liquid with a density one-tenth that of brass.

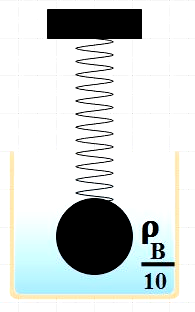
By doing so, in addition to the brass ball’s weight and restoring force acting, the system also has buoyant force acting in the upward direction. However, the mass of the ball as well as the spring constant still remains constant. Therefore, from (4), the time period also remains the same even when this system is immersed in the liquid.

So, the correct answer is “Option C”.

Note:
When we immerse the system in the liquid, there is also buoyant force acting on the brass ball in addition to all the other forces. This fact may often make you think that the time period will also be affected during the immersion. But remember, all that time period of a spring mass system depends on its mass of the body and spring constant. Effective acceleration due to gravity is changed when immersed, but our time period here is independent of g.