Question

A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed \[\sqrt {gl} \]. Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.

Answer 1

Hint:First, according to the given statement, draw a rough diagram representing the given parameters. First find the height difference between the initial point and the final point of the particle which is inclined at an angle at an instant. Then using the rectilinear motion formula of the particles we can find the final speed as the initial speed is known to us. Now at the final point, balance all the force and write an equation by equating tensional force to the weight of the particle. Now on further solving we can find the inclination of the string.

Complete step by step answer:
As per the problem a heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed \[\sqrt {gl} \]. We need to calculate the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.

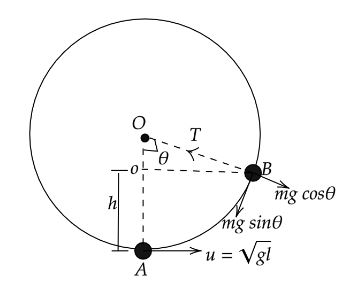
From the figure point A is the initial point of the particle which is hanging from a fixed point by a light string and point B is the final point of the particle where the tension is equal to the weight of the particle.

From the figure the height between two positions can be written as,
$h = OA - Oo$
Where, OA is the length of string which is equal to l.
From the figure,
$Oo = l\cos \theta $
Putting this values we will get,
$h = l - l\cos \theta $
$ \Rightarrow h = l\left( {1 - \cos \theta } \right)$
We know the initial velocity of the particle as $u = \sqrt {gl} $ after some time it travelled a distance of h from the initial point hence, $h = l\left( {1 - \cos \theta } \right)$ and the acceleration of the particle is due to gravity which equals to g.

Now using rectilinear motion on the particle we can write,
${v^2} - {u^2} = 2as$
Putting the values we will get,
${v^2} - {\left( {\sqrt {gl} } \right)^2} = 2gh$
$ \Rightarrow {v^2} - gl = 2gl\left( {1 - \cos \theta } \right)$
Rearranging and on further solving we will get,
$v = \sqrt {gl - 2gl\left( {1 - \cos \theta } \right)} \ldots \ldots \left( 1 \right)$
Now at point B balancing the forces we will get,
$T - mg\cos \theta = \dfrac{{m{v^2}}}{r}$
Here, Radius of the circle r is equal to the stop length of the string l. Tension is equal to the weight of the particle.

Final velocity of the particle is known to us. Hence on putting all theses in the above equation we will get,
$mg - mg\cos \theta = \dfrac{{m\left( {gl - 2gl\left( {1 - \cos \theta } \right)} \right)}}{l}$
Cancelling the common terms we will get,
$1 - \cos \theta = 1 - 2\left( {1 - \cos \theta } \right)$
$ \Rightarrow - \cos \theta = - 2\left( {1 - \cos \theta } \right) \\
\Rightarrow \cos \theta = 2\left( {1 - \cos \theta } \right)$

Rearranging the above equation we will get,
$3\cos \theta = 2 \Rightarrow \cos \theta = \dfrac{2}{3}$’
Hence the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle is $\theta = {\cos ^{ - 1}}\dfrac{2}{3}$.
Putting this $\cos \theta $ value in the equation $\left( 1 \right)$ we will get,
$v = \sqrt {gl - 2gl\left( {1 - \dfrac{2}{3}} \right)} $
$ \Rightarrow v = \sqrt {gl - 2gl\dfrac{1}{3}} \\
\therefore v= \sqrt {\dfrac{{gl}}{3}} $

Hence the speed of the particle at the instant of the motion when the tension in the string is equal to the weight of the particle is $v = \sqrt {\dfrac{{gl}}{3}} $.

Note:Here we have taken the acceleration of the final point as negative as the particle is moving upward while the acceleration due to gravity is acting downward on the particles. Always make a free body diagram to solve this kind of problem. Free body diagram is a graphical illustration used to visualize the applied forces on a body.