
A hemispherical bowl is made of brass, 0.25 cm thickness. The inner radius of the bowl is 5 cm. Find the ratio of the outer surface area to the inner surface area.
Answer
524.4k+ views
Hint: First of all, find the outer radius of the bowl by adding the inner radius and thickness of the bowl. Now, find the surface area of the bowl by using
Complete step-by-step solution -
Here, we are given a hemispherical bowl made of brass having 0.25 cm thickness. Its inner radius is 5 cm. We have to find the ratio of its outer surface area to the inner surface area. Let us, first of all, draw the side and front view of the hemispherical bowl made of brass to visualize the question.
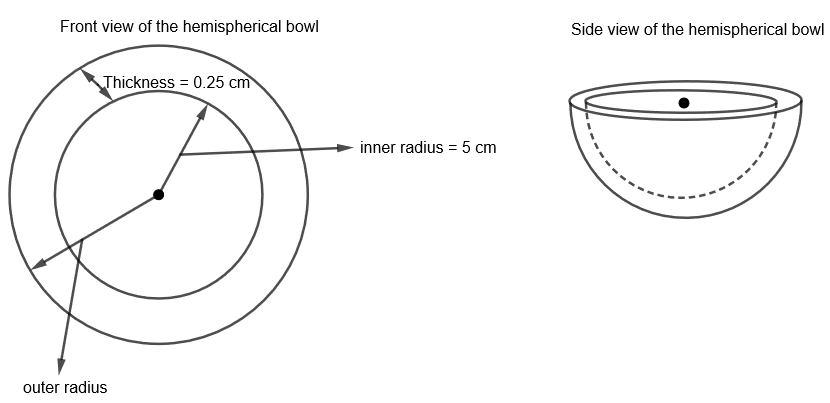
Here, we are given that the inner radius of the hemispherical bowl,
The thickness of hemispherical bowl = 0.25 cm
So, we get the outer radius of the hemispherical bowl,
= 5 cm + 0.25 cm
Now, we know that the surface area of the hemispherical bowl
By substituting the value of
Also, we get the outer surface area of the hemispherical bowl,
By substituting the value of
So, we get the ratio of the outer surface area of the bowl to the inner surface area of the bowl as,
By substituting the value of
Hence, we get the ratio of the outer surface area of the bowl to the inner surface area of the bowl as 1.1025.
Note: By looking at the hemisphere and surface area, some students make this mistake of writing the surface area as
Complete step-by-step solution -
Here, we are given a hemispherical bowl made of brass having 0.25 cm thickness. Its inner radius is 5 cm. We have to find the ratio of its outer surface area to the inner surface area. Let us, first of all, draw the side and front view of the hemispherical bowl made of brass to visualize the question.

Here, we are given that the inner radius of the hemispherical bowl,
The thickness of hemispherical bowl = 0.25 cm
So, we get the outer radius of the hemispherical bowl,
= 5 cm + 0.25 cm
Now, we know that the surface area of the hemispherical bowl
By substituting the value of
Also, we get the outer surface area of the hemispherical bowl,
By substituting the value of
So, we get the ratio of the outer surface area of the bowl to the inner surface area of the bowl as,
By substituting the value of
Hence, we get the ratio of the outer surface area of the bowl to the inner surface area of the bowl as 1.1025.
Note: By looking at the hemisphere and surface area, some students make this mistake of writing the surface area as
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE




