Question

A hollow cone with base radius \[acm\] and height \[bcm\] is placed on a table. Show that the volume of the largest cylinder that can be hidden underneath is \[\dfrac{4}{9}\] times the volume of the cone.

Answer 1

Hint: A cylinder is a solid figure, with a circular or oval base or cross section and straight and parallel sides. It is a closed solid figure with two circular bases that are connected by a curved surface. A cone is a solid three-dimensional figure with a flat circular base from which it tapers smoothly to a point known as the vertex.

Complete step by step solution:

Formulas used in the solution are:
Volume of cylinder \[V = \pi {r^2}h\]
Where \[r\] is the radius of base of the cylinder and \[h\] is the height of the cylinder.
Volume of cone \[ = \dfrac{1}{3}\pi {r^2}h\]
Where \[r\] is the radius of base of the cone and \[h\] is the height of the cone.
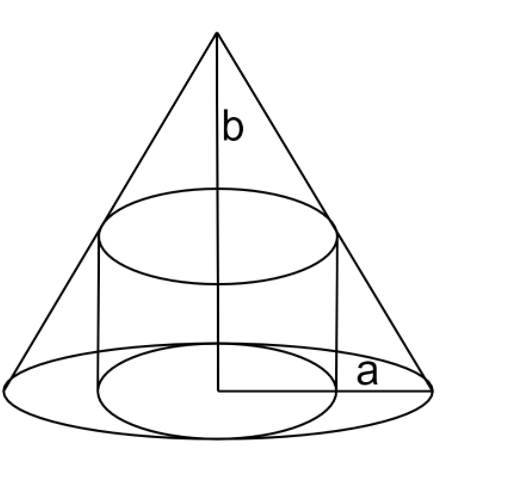
Here in this question we are given the following:
The height of cone \[ = h = b\]
The base radius \[ = r = a\]
The base radius of cylinder \[ = r\]
The height of cylinder \[ = h\]
Using similar triangles:
 \[\dfrac{h}{{a - r}} = \dfrac{b}{a}\]
Hence we get ,
 \[h = \dfrac{b}{a}\left( {a - r} \right) = b - \dfrac{b}{a}r\]
Volume of cylinder \[V = \pi {r^2}h\]
Putting value of \[h\] we get ,
 \[V = \pi {r^2}\left[ {b - \dfrac{b}{a}r} \right] \]
 \[ = \pi b{r^2} - \dfrac{{\pi b{r^3}}}{a}\]
On differentiating both sides with respect to \[r\] we get ,
 \[\dfrac{{dV}}{{dx}} = \dfrac{{2\pi abr - 3\pi b{r^2}}}{a}\] … \[(1)\]
Putting \[\dfrac{{dV}}{{dx}} = 0\]
We get \[\pi br(2a - 3r) = 0\]
Hence we get \[r = \dfrac{{2a}}{3}\]
Differentiating \[(1)\] with respect to \[r\] we get ,
 \[\dfrac{{{d^2}V}}{{d{r^2}}} = 2\pi b - \dfrac{{6\pi br}}{a}\]
Putting value of \[r = \dfrac{{2a}}{3}\]
 \[\dfrac{{{d^2}V}}{{d{r^2}}} = 2\pi b - \dfrac{{6\pi b}}{a}\left( {\dfrac{{2a}}{3}} \right)\]
 \[ = - 2\pi b\]
Therefore \[r = \dfrac{{2a}}{3}\] is a maximum point.
So volume is maximum at \[r = \dfrac{{2a}}{3}\] .
Therefore we get \[h = \dfrac{b}{a}\left( {a - \dfrac{{2a}}{3}} \right) = \dfrac{b}{3}\]
Volume of cylinder \[ = \pi {r^2}h = \pi {\left( {\dfrac{{2a}}{3}} \right)^2}\left( {\dfrac{b}{3}} \right)\]
 \[ = \dfrac{4}{9}\left( {\dfrac{1}{3}\pi {a^2}b} \right)\]
 \[ = \dfrac{4}{9}\] (volume of cone)
Hence showed.

Note: A cylinder is a solid figure, with a circular or oval base or cross section and straight and parallel sides. It is a closed solid figure with two circular bases that are connected by a curved surface. A cone is a solid three-dimensional figure with a flat circular base from which it tapers smoothly to a point known as the vertex.