
A homogeneous solid cylindrical roller of radius
(A)
(B)
(C)
(D)
Answer
482.4k+ views
1 likes
Hint From the formula for torque given by product of the moment of inertia and the angular acceleration. The torque is also given by the product of the force and the radius. So equating we get the angular acceleration.
In this solution we will be using the following formula,
where
again
where
Complete step by step answer
In the question we are given a homogeneous solid cylinder that is given a horizontal force. So we can draw the diagram as,
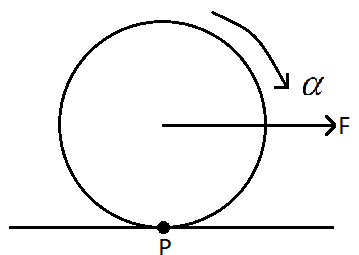
The cylinder, as we can see from the diagram, is touching at the point P. Now the torque is given as the product of the moment of inertia and the angular acceleration. So we can write,
Now the moment of inertia of a solid homogeneous cylinder about an axis passing through its center and along the length is given by the formula,
So substituting this we get,
Now the torque on the cylinder due to the force that is acting on it horizontally is given by the product of the force and the distance of the point of contact from the axis of rotation. Hence we have,
So we can equate the two values of torque as,
Keeping only the
On cancelling the
Hence the angular acceleration is
So the correct answer is option (C).
Note
The moment of inertia of a rigid body is the quantity that determines the torque needed for the required angular acceleration about a rotational axis. It is equivalent to the way mass determines the force needed for desired acceleration.
In this solution we will be using the following formula,
where
again
where
Complete step by step answer
In the question we are given a homogeneous solid cylinder that is given a horizontal force. So we can draw the diagram as,

The cylinder, as we can see from the diagram, is touching at the point P. Now the torque is given as the product of the moment of inertia and the angular acceleration. So we can write,
Now the moment of inertia of a solid homogeneous cylinder about an axis passing through its center and along the length is given by the formula,
So substituting this we get,
Now the torque on the cylinder due to the force that is acting on it horizontally is given by the product of the force and the distance of the point of contact from the axis of rotation. Hence we have,
So we can equate the two values of torque as,
Keeping only the
On cancelling the
Hence the angular acceleration is
So the correct answer is option (C).
Note
The moment of inertia of a rigid body is the quantity that determines the torque needed for the required angular acceleration about a rotational axis. It is equivalent to the way mass determines the force needed for desired acceleration.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




