
A hyperbola having the transverse axis of length
Answer
433.8k+ views
Hint: In this problem we need to find the equation of the hyperbola which is confocal with the given ellipse and the having the transverse axis length
Complete step by step answer:
Given equation of the ellipse is
Dividing the above equation with
Comparing the above equation with
Now the eccentricity of the ellipse is given by
Now the focus of the ellipse is given by
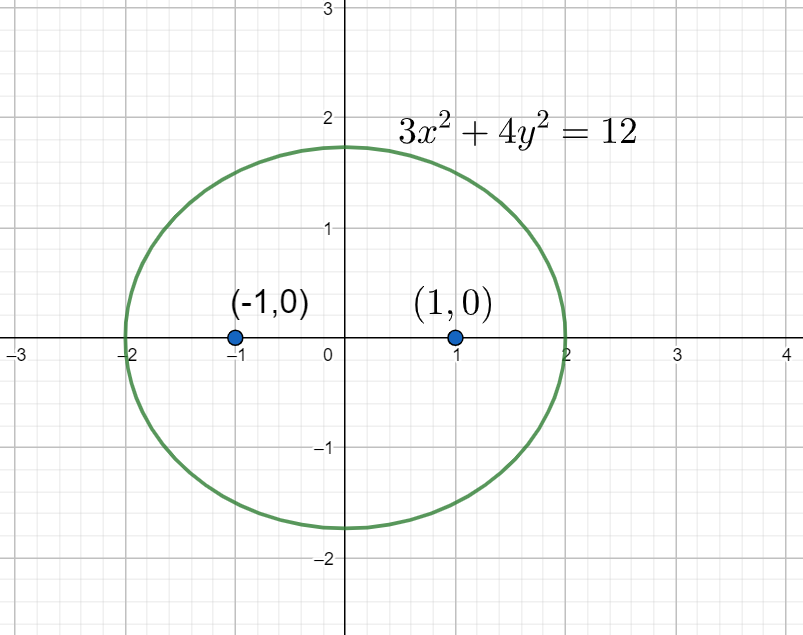
Given the both the required hyperbola and the ellipse are confocal that means the focus of the ellipse and hyperbola are same. So, the focus of the required hyperbola is
Let us assume the parameters of the required hyperbola as
Given that the length of traverse axis of the hyperbola is
We have the focus of the hyperbola as
Substituting the value
Now calculating the value of
Simplifying the above equation and using the trigonometric formula
From the trigonometric identity
Substituting the trigonometric formula
Now the equation of the hyperbola is given by
Hence the equation of the required hyperbola is
Note: In this problem they have mentioned that both the required hyperbola and the ellipse are confocal so we have taken the focus of both the shapes as equal. Sometimes they may give that both are concentric then we will take the eccentricity of both the shapes as equal.
Complete step by step answer:
Given equation of the ellipse is
Dividing the above equation with
Comparing the above equation with
Now the eccentricity of the ellipse is given by
Now the focus of the ellipse is given by

Given the both the required hyperbola and the ellipse are confocal that means the focus of the ellipse and hyperbola are same. So, the focus of the required hyperbola is
Let us assume the parameters of the required hyperbola as
Given that the length of traverse axis of the hyperbola is
We have the focus of the hyperbola as
Substituting the value
Now calculating the value of
Simplifying the above equation and using the trigonometric formula
From the trigonometric identity
Substituting the trigonometric formula
Now the equation of the hyperbola is given by
Hence the equation of the required hyperbola is
Note: In this problem they have mentioned that both the required hyperbola and the ellipse are confocal so we have taken the focus of both the shapes as equal. Sometimes they may give that both are concentric then we will take the eccentricity of both the shapes as equal.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




