
A hyperbola whose transverse axis is along the major axis of the ellipse $\dfrac{{{x}^{2}}}{3}+\dfrac{{{y}^{2}}}{4}=4$ and has vertices at the focus of the ellipse. If the eccentricity of the hyperbola is $\dfrac{3}{2}$, then which of the following points do not lie on it
[a] $\left( \sqrt{5},2\sqrt{2} \right)$
[b] (0,2)
[c] $\left( 5,2\sqrt{3} \right)$
[d] $\left( 10,2\sqrt{3} \right)$
Answer
593.4k+ views
Hint:The transverse axis of a hyperbola is the axis of the hyperbola that passes through the foci of the hyperbola. If $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is the equation of an ellipse, then the major axis is x-axis if a>b and the major axis is y-axis if ${a}<{b}$. Use this fact to find the major axis of the hyperbola. Use the fact that if e is the eccentricity of the ellipse, then the coordinates of foci are (0, be) and (0,-be) and ${{a}^{2}}={{b}^{2}}\left( 1-{{e}^{2}} \right)$.
Also, the vertices of the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1$ are (0,b) and (0,-b) and the eccentricity satisfies ${{a}^{2}}={{b}^{2}}\left( {{e}^{2}}-1 \right)$
Complete step-by-step answer:
We know Equation of ellipse
$\dfrac{{{x}^{2}}}{3}+\dfrac{{{y}^{2}}}{4}=4$
We need to write the equation in $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ form. Hence we divide the both sides of the equation by 4. Hence, we have
$\dfrac{{{x}^{2}}}{12}+\dfrac{{{y}^{2}}}{16}=1$
Here $a=\sqrt{12}$ and $b=\sqrt{16}=4$
Hence aHence the major axis is the y-axis.
Hence the transverse axis of the hyperbola is the y-axis[As according to the question the transverse axis coincides with the major axis of the ellipse]
We know that eccentricity e of the ellipse is given by ${{a}^{2}}={{b}^{2}}\left( 1-{{e}^{2}} \right)$
Hence, we have
$\begin{align}
& 12=16\left( 1-{{e}^{2}} \right) \\
& \Rightarrow \dfrac{3}{4}=1-{{e}^{2}} \\
& \Rightarrow e=\dfrac{1}{2} \\
\end{align}$
Hence the foci of the ellipse are $\left( 0,4\times \dfrac{1}{2} \right)=\left( 0,2 \right)$ and $\left( 0,-4\times \dfrac{1}{2} \right)=\left( 0,-2 \right)${Because coordinates of the foci are given by (0,be) and (0,-be)}
Let the equation of hyperbola be $\dfrac{{{y}^{2}}}{{{b}^{2}}}-\dfrac{{{x}^{2}}}{{{a}^{2}}}=1$
We know that the coordinates of vertices are given by (0,b) and (0,-b)
Hence, we have $\left( 0,b \right)=\left( 0,2 \right)${As the vertices of the hyperbola coincide with the foci of the ellipse}.
Comparing y coordinates, we get
$b=2$.
Also, the eccentricity of the hyperbola is given by ${{a}^{2}}={{b}^{2}}\left( {{e}^{2}}-1 \right)\Rightarrow a=b\sqrt{{{e}^{2}}-1}$
Since $e=\sqrt{5}$ (given) and $b=2$, we have
Hence $a=b\sqrt{{{e}^{2}}-1}=2\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}-1}=\sqrt{5}$
Hence the equation of the hyperbola is $\dfrac{{{y}^{2}}}{{{2}^{2}}}-\dfrac{{{x}^{2}}}{{{\left( \sqrt{5} \right)}^{2}}}=1\Rightarrow \dfrac{{{y}^{2}}}{4}-\dfrac{{{x}^{2}}}{5}=1$
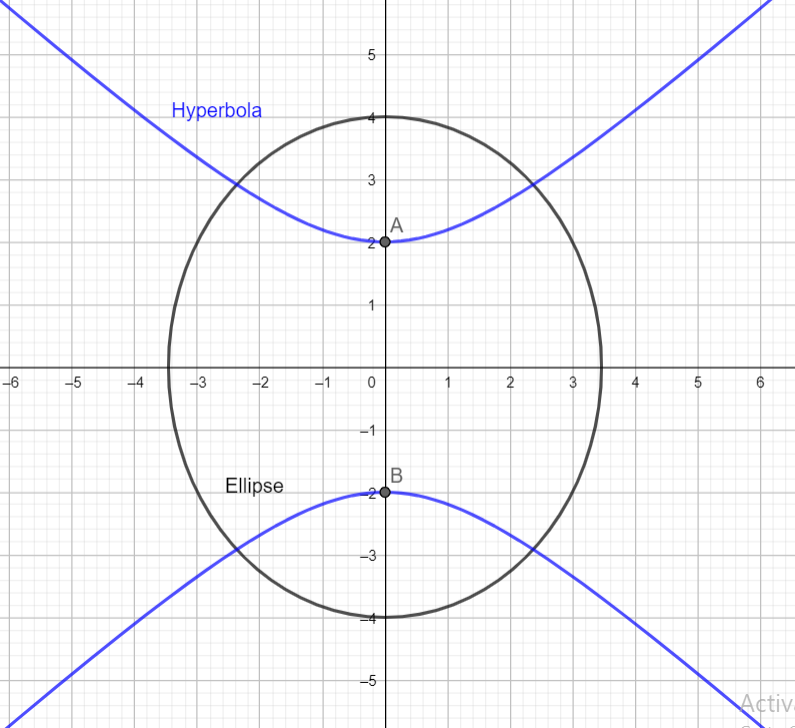
Clearly $\left( 5,2\sqrt{3} \right)$ does not satisfy the equation of the hyperbola as $\dfrac{{{\left( 2\sqrt{3} \right)}^{2}}}{4}-\dfrac{{{\left( 5 \right)}^{2}}}{5}=3-5=-2\ne 1$.
Hence $\left( 5,2\sqrt{3} \right)$ does not lie on the hyperbola.
Hence option [c] is correct.
Note: A point lies on a curve if and only if it satisfies the equation of that curve, This is why we found the equation of hyperbola first and then checked whether these points satisfy the equation of the hyperbola.
Graphically this can be seen as
Also, the vertices of the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1$ are (0,b) and (0,-b) and the eccentricity satisfies ${{a}^{2}}={{b}^{2}}\left( {{e}^{2}}-1 \right)$
Complete step-by-step answer:
We know Equation of ellipse
$\dfrac{{{x}^{2}}}{3}+\dfrac{{{y}^{2}}}{4}=4$
We need to write the equation in $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ form. Hence we divide the both sides of the equation by 4. Hence, we have
$\dfrac{{{x}^{2}}}{12}+\dfrac{{{y}^{2}}}{16}=1$
Here $a=\sqrt{12}$ and $b=\sqrt{16}=4$
Hence a
Hence the transverse axis of the hyperbola is the y-axis[As according to the question the transverse axis coincides with the major axis of the ellipse]
We know that eccentricity e of the ellipse is given by ${{a}^{2}}={{b}^{2}}\left( 1-{{e}^{2}} \right)$
Hence, we have
$\begin{align}
& 12=16\left( 1-{{e}^{2}} \right) \\
& \Rightarrow \dfrac{3}{4}=1-{{e}^{2}} \\
& \Rightarrow e=\dfrac{1}{2} \\
\end{align}$
Hence the foci of the ellipse are $\left( 0,4\times \dfrac{1}{2} \right)=\left( 0,2 \right)$ and $\left( 0,-4\times \dfrac{1}{2} \right)=\left( 0,-2 \right)${Because coordinates of the foci are given by (0,be) and (0,-be)}
Let the equation of hyperbola be $\dfrac{{{y}^{2}}}{{{b}^{2}}}-\dfrac{{{x}^{2}}}{{{a}^{2}}}=1$
We know that the coordinates of vertices are given by (0,b) and (0,-b)
Hence, we have $\left( 0,b \right)=\left( 0,2 \right)${As the vertices of the hyperbola coincide with the foci of the ellipse}.
Comparing y coordinates, we get
$b=2$.
Also, the eccentricity of the hyperbola is given by ${{a}^{2}}={{b}^{2}}\left( {{e}^{2}}-1 \right)\Rightarrow a=b\sqrt{{{e}^{2}}-1}$
Since $e=\sqrt{5}$ (given) and $b=2$, we have
Hence $a=b\sqrt{{{e}^{2}}-1}=2\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}-1}=\sqrt{5}$
Hence the equation of the hyperbola is $\dfrac{{{y}^{2}}}{{{2}^{2}}}-\dfrac{{{x}^{2}}}{{{\left( \sqrt{5} \right)}^{2}}}=1\Rightarrow \dfrac{{{y}^{2}}}{4}-\dfrac{{{x}^{2}}}{5}=1$

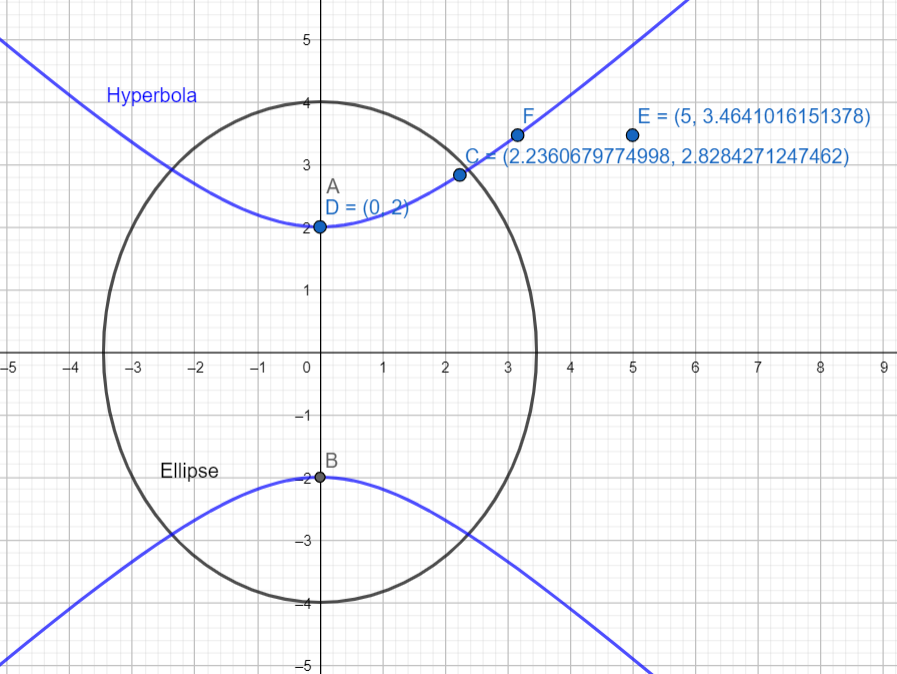
Clearly $\left( 5,2\sqrt{3} \right)$ does not satisfy the equation of the hyperbola as $\dfrac{{{\left( 2\sqrt{3} \right)}^{2}}}{4}-\dfrac{{{\left( 5 \right)}^{2}}}{5}=3-5=-2\ne 1$.
Hence $\left( 5,2\sqrt{3} \right)$ does not lie on the hyperbola.
Hence option [c] is correct.
Note: A point lies on a curve if and only if it satisfies the equation of that curve, This is why we found the equation of hyperbola first and then checked whether these points satisfy the equation of the hyperbola.
Graphically this can be seen as

Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is a periderm How does periderm formation take class 11 biology CBSE




