Question

A jet airliner moving initially at \[300mi/h\] due east enters a region where the wind is blowing at \[100mi/h\] towards the direction \[{30^0}\] north of east. What is the new speed and direction of the aircraft relative to the ground?

Answer 1

Hint:The motion of the wind will affect the motion of aircraft .This phenomenon is known as Wind effect. The speed and direction of wind will change both speed and direction of the plane due to this wind effect.Using the air as the intermediate reference frame, ground speed can be given by:
\[{\overrightarrow V _{PG}} = {\overrightarrow V _{PA}} + {\overrightarrow V _{AG}}\]
 

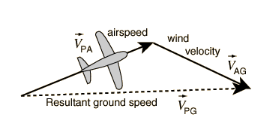
The velocity of the plane with respect to the ground is equal to the velocity of the plane with respect to the air plus the velocity of air with respect to the ground.In above question, first we find the vector form of velocity of the plane. Then we find the vector form of velocity of the air with inclination (angle in degree given). Then we add 2 velocities by vector sum. The resultant speed is magnitude of vector some and direction is \[\arctan \] or \[{\tan ^{ - 1}}\].

Complete step by step answer:
Wind speed = \[100mi/h\], direction of wind = \[{30^0}\] north to east,
speed of airliner=\[300mi/h\], direction of airliner = toward east.
vector form of speed of airliner (the air speed of the plane)= \[300\hat i\]
vector form of speed of wind with \[{30^0}\] direction, i.e.,
Wind speed relative to ground=\[100\cos {30^0}\hat i + 100\sin {30^0}\hat j\]
\[\Rightarrow 86.6\hat i + 50\hat j\]
Sum of two vector speed=\[300\hat i + (86.6\hat i + 50\hat j)\]
\[\Rightarrow 386.6\hat i + 50\hat j\]
Hence, new speed of aircraft= \[\sqrt {{{386.6}^2} + {{50}^2}} \] \[mi/h\]= \[389.82\]\[mi/h\] and new direction of the aircraft relative to the ground= \[\arctan \] or \[{\tan ^{ - 1}}\] of \[\dfrac{{50}}{{386.6}}\]
\[\Rightarrow{\tan ^{ - 1}}\left( {\dfrac{{50}}{{386.6}}} \right)\]
\[\therefore{7.37^0}\] in the direction north of east.

Hence, aircraft will move with the speed of \[389.82\]\[mi/h\] in the direction of \[{7.37^0}\] north of east.

Additional information:
When adding velocities, we have been careful to specify that the velocity is relative to some reference frame. These velocities are called relative velocities. When two objects are moving, then relative velocity is defined as the velocity of an object relative to the second object. Second object might be stationary, moving with higher velocity, less velocity, moving with same velocity or moving in the opposite direction.

Note:When adding two vectors, students can make mistakes. For example one vector is \[a\hat i + b\hat j\] and second is \[x\hat i + y\hat j\]. Then the resultant vector is \[(a + x)\hat i + (b + y)\hat j\]. Students should be careful about addition of vectors, otherwise the answer will be incorrect.