Question

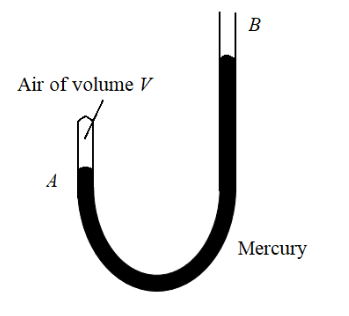
A J-tube shown in the figure contains a volume V of dry air trapped in arm A of the tube. The atmospheric pressure is H cm of mercury. When more mercury is poured in arm B, the volume of the enclosed air and its pressure undergo a change. What should be the difference in mercury levels in the arms so as to reduce the volume of air to V/2?

(A) $H cm$
(B) \[\dfrac{H}{2}\,{\text{cm}}\]
(C) \[2H\,{\text{cm}}\]
(D) \[\dfrac{H}{{30}}\,{\text{cm}}\]

Answer 1

Hint:Refer to the ideal gas law to determine the pressure at arm A. Use the formula to calculate the pressure below the height h of the liquid column of density \[\rho \].

Complete step by step answer:
According to Ideal gas law, the product of pressure and volume is constant.
Therefore, we can write,
\[\Rightarrow{P_1}{V_1} = {P_2}{V_2}\]
Here, \[{V_1}\] is the volume of the arm A at atmospheric pressure \[{P_1}\] and \[{V_2}\] is the volume of the arm A at pressure \[{P_2}\].
The initial volume is V and the final volume is \[\dfrac{V}{2}\]. The pressure \[{P_1}\] is the atmospheric pressure P.
Therefore, the above equation becomes,
\[\Rightarrow PV = {P_2}\dfrac{V}{2}\]
\[ \Rightarrow {p_2} = 2P\]
We know that the pressure below the height H is,
 \[ \Rightarrow P = H\rho g\]
Therefore,
\[\Rightarrow {p_2} = 2H\rho g\]
Here, \[\rho \] is the density of the liquid and g is the acceleration due to gravity.
Let the height of the mercury column is x. The pressure below the height x is the sum of atmospheric pressure and the pressure due to the mercury column above it. We have determined the pressure at the arm A which is 2P.
Therefore,
\[\Rightarrow 2P = {P_0} + x\rho g\]
We have given, the atmospheric pressure is H cm of mercury. Therefore, the atmospheric pressure is,
\[\Rightarrow{P_0} = H\rho g\]
Therefore, the pressure at arm A is,
\[ \Rightarrow 2H\rho g = H\rho g + x\rho g\]
\[ \Rightarrow 2H\rho g = \rho g\left( {H + x} \right)\]
\[ \Rightarrow 2H = \left( {H + x} \right)\]
\[ \Rightarrow\therefore x = h\]

So, the correct answer is option (A).

Note:The pressure inside an open liquid column is the addition of atmospheric pressure over the surface of the liquid and the pressure due to liquid above that point.