Question

A ladder 10m long rests against a vertical wall with the lower end on the horizontal ground. The lower end of the ladder is pulled along the ground away from the wall at a rate of 3cm/sec. The height of upper end while it is descending at the rate of 4cm/sec is
A. $4\sqrt 3 $m
B. $5\sqrt 3 $m
C. $5\sqrt 2 $m
D. 6m

Answer 1

Hint: In this question, first we will draw a diagram for the question. After this we will assume the length BA as x and corresponding rate as $\dfrac{{dx}}{{dt}}$ and similarly do for side BC. Then we apply the Pythagoras theorem in triangle ABC and differentiate further to get a new equation.

Complete step-by-step answer:
The diagram for question is given below:

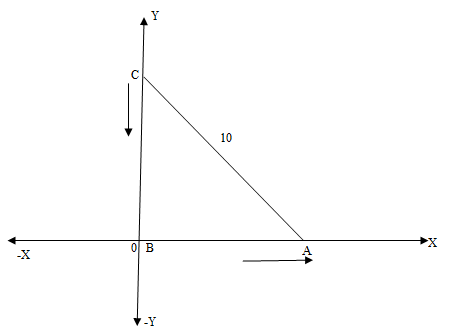
It is given that the lower portion of the ladder is pulled away from the ground that is point A is being pulled. So length AB must be changing.
 So, let the length of AB = x cm.

Now change in length AB with time will be given as:
$\dfrac{{d(AB)}}{{dt}} = \dfrac{{dx}}{{dt}}$ . This is the rate of pulling away the ladder on ground which is given as 3cm/sec.
$\therefore \dfrac{{dx}}{{dt}} = 3$ …………………………………. (1)
Now from the figure it is clear that if A is pulled away from ground then point C will be dragged towards ground whose rate is given as 4cm/sec.
Let length of BC = y cm
Thus change in length of CB with time is given as:
$\dfrac{{d(BC)}}{{dt}} = - \dfrac{{dy}}{{dt}}$ = 4 (Negative because it’s reducing with time)…………….. (2)
Now clearly $\vartriangle ABC$ is right angled at B so let’s apply Pythagoras theorem.
According to Pythagoras theorem,
$A{B^2} + B{C^2} = C{A^2}$
So we can write:
${x^2} + {y^2} = {10^2} = 100$ ………………….. (3)
Differentiating equation (3) with respect to ‘t’, we get:
$2x\dfrac{{dx}}{{dt}} + 2y\dfrac{{dy}}{{dt}} = 0$
Putting the values from equation 1 and equation 2, we get:
2x(3)+2y(-4) = 0
$ \Rightarrow x = \dfrac{{4y}}{3}$
Now putting this x in equation 3, we get:
$\dfrac{{16}}{9}{y^2} + {y^2} = 100$
$ \Rightarrow \dfrac{{25}}{9}{y^2} = 100$
On further solving the above equation, we get:
${y^2} = \dfrac{{100 \times 9}}{{25}} = 36$
$ \Rightarrow y = \pm 6$
Since y is the length of CB and thus it can’t be negative.
 Hence, y= 6 cm.
Thus option (d) is the right answer.

So, the correct answer is “Option (d)”.

Note: Whenever the rate of change of length with time is being told in a problem statement, make sure that if the length is increasing with time (generally when pulled) so the rate change is positive and if it is pushed then eventually it’s decreasing with time hence the rate change should be negative. You should remember the Pythagoras theorem which is applied in the right triangle.