Question

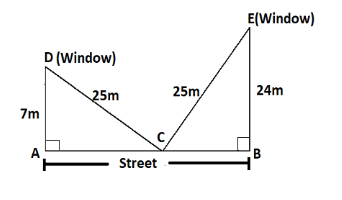
A ladder \[25m\] long reaches a window which is \[7m\] above the ground. On one side of the street. Keeping its foot at the same point, the ladder is turned t the other side of the street to reach a window a height of \[24m\] . Find the width (in metre) of the street.

Answer 1

Hint: Here, the word problem is converted into mathematical expression which is defined with diagrammatic explanation of a long ladder reaches a window, keeping its foot at the same point, the ladder is turned other side of the street and to calculate the width of the street by using pythagoras theorem.

Complete step-by-step answer:
Given,
A ladder \[25\;m\] long reaches a window, \[CD\]
The window above the ground, \[AD\] is \[7\;m\]
On the other side of street,
A ladder \[25\;m\] long reaches a window, \[CE\]
Street to reach a window height, \[\;EB\] is \[24\;m\]

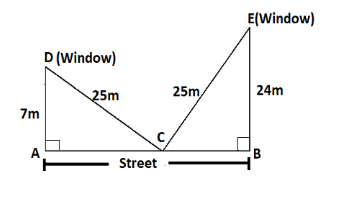
To find the width of the street, \[AB\]
From the diagram \[\Delta ADC\] and \[\Delta BEC\] are right angled triangles.
By using Pythagoras theorem, we get
Pythagora's theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
In \[\Delta ADC\] , we have
 \[CD{\;^2} = A{C^2} + A{D^2}\]
By substitute the values from the diagram, we get
 \[{25^2} = A{C^2} + {7^2}\]
To simplify, we get
 \[
  625 - 49 = A{C^2} \\
  A{C^2} = 576 = {24^2} \;
 \]
Take square root on both sides, then we get
 \[AC = 24\]
Therefore, the value of \[AC = 24\] .
In \[\Delta BEC\] , we have
 \[E{C^2} = B{C^2} + B{E^2}\]
By substitute the values from the diagram, we get
 \[
  {25^2} = B{C^2} + {24^2} \\
  625 - 576 = B{C^2} \;
\]
To simplify it, we get
 \[
  B{C^2} = 49 \\
  B{C^2} = {7^2} \;
 \]
Take square root on both sides, then we get
 \[BC = 7\]
To find the width of the street, we get
 \[AB = AC + BC = 24 + 7\]
 \[AB = 31\;m\]
Therefore, the width of the street is \[31m\]
So, the correct answer is “ \[31\;m\] ”.

Note: By solving this problem by using Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.