
A ladder has rungs 25cm apart. The rungs decrease uniformly in the length from 45cm at the bottom to 25cm at the top. If the top and bottom rungs are
(a) 280cm
(b) 320cm
(c) 250cm
(d) 385cm
Answer
511.5k+ views
Hint: In order to solve this problem, we need to find the total number of rungs. To find this we formula we need is
Complete step-by-step answer:
We are given that the distance between two rungs is 25cm.
The rungs decrease uniformly starting with 45cm at the bottom and 25cm at the top.
We know that the gap between two rungs is 25cm.
To understand better, we need to draw a rough figure.
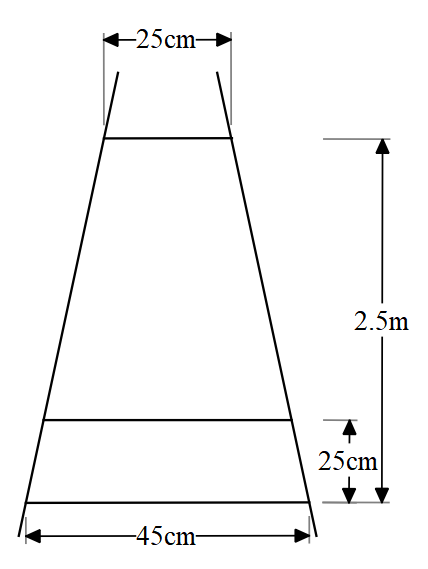
We are also given that the total length of the ladder is
We need to convert this length into centimetres.
Total length =
Total length =
We know the spacing between the rungs and the total length of the ladder so we can find the number of rungs.
The formula for that is
Substituting the values we get,
This problem can be now solved by arithmetic progression. And we need to find the total wood required for rungs.
In arithmetic progression,
Total wood required for rungs = Sum of
The formula for that is,
Where
Substituting the values as
Therefore, the length of the wood required is 385cm.
Note: In the formula for the total number of rungs we need to add 1 because we tend to miss the first rungs as we divide the total length by distance between 2 rungs. Also, we need to take care that the length of the ladder is given in metres and the rest of the dimensions are in centimetres. We need to convert meters into centimetres.
Complete step-by-step answer:
We are given that the distance between two rungs is 25cm.
The rungs decrease uniformly starting with 45cm at the bottom and 25cm at the top.
We know that the gap between two rungs is 25cm.
To understand better, we need to draw a rough figure.

We are also given that the total length of the ladder is
We need to convert this length into centimetres.
Total length =
Total length =
We know the spacing between the rungs and the total length of the ladder so we can find the number of rungs.
The formula for that is
Substituting the values we get,
This problem can be now solved by arithmetic progression. And we need to find the total wood required for rungs.
In arithmetic progression,
Total wood required for rungs = Sum of
The formula for that is,
Where
Substituting the values as
Therefore, the length of the wood required is 385cm.
Note: In the formula for the total number of rungs we need to add 1 because we tend to miss the first rungs as we divide the total length by distance between 2 rungs. Also, we need to take care that the length of the ladder is given in metres and the rest of the dimensions are in centimetres. We need to convert meters into centimetres.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




