
A ladder has rungs 25cm apart. The rungs decrease uniformly in length from 45cm at the bottom to 25cm at the top. If the top and the bottom rungs are 2.5 m apart, what is the length of the wood required for the rungs?
Answer
511.5k+ views
Hint: Apply the sum of n terms of the AP, which is given by the formula
Complete step-by-step solution -
In the question, we are given that the ladder has rungs 25 cm apart. The first rung is length 45 cm and the last rung is of length 25 cm. So, we have to find the total length of the wood required for all the rungs.
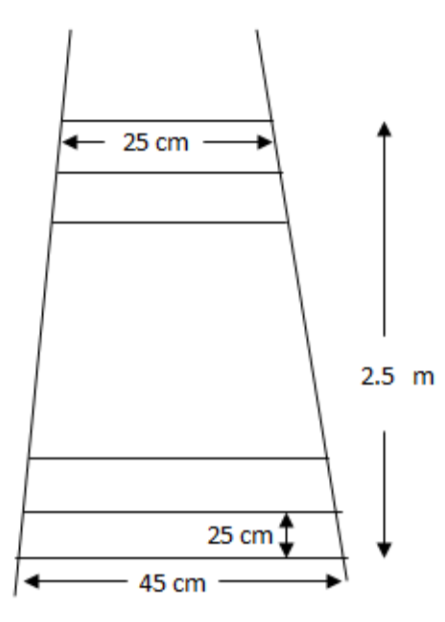
So, here the rungs length of the ladder form an Arithmetic series with the first term a=45 cm and last term as l=25cm.
Now, in order to find the total length of the wood required for all the rungs, we have to find the sum of this series for n number of terms. Now n, is the total number of rungs.
So we will first find n here. Now, the distance between the first and the last rung is given as 2.5 m or 250 cm and distance between the two consecutive rungs are 25 cm.
So, The total number of rungs, it is required to find the total length of the rung, as these rungs length are in AP, and each rung represents each term of the AP. Using the concept of AP, if we know the sum , then we can find the number of terms, which represents the number of rungs here.
Next, we will find the sum of all the length of all the rungs by the formula:
So the total length of the wood required for all the rungs will be 385 cm.
Note: It can be noted that the sum of n terms of the AP can be found using the formula:
Complete step-by-step solution -
In the question, we are given that the ladder has rungs 25 cm apart. The first rung is length 45 cm and the last rung is of length 25 cm. So, we have to find the total length of the wood required for all the rungs.

So, here the rungs length of the ladder form an Arithmetic series with the first term a=45 cm and last term as l=25cm.
Now, in order to find the total length of the wood required for all the rungs, we have to find the sum of this series for n number of terms. Now n, is the total number of rungs.
So we will first find n here. Now, the distance between the first and the last rung is given as 2.5 m or 250 cm and distance between the two consecutive rungs are 25 cm.
So, The total number of rungs, it is required to find the total length of the rung, as these rungs length are in AP, and each rung represents each term of the AP. Using the concept of AP, if we know the sum , then we can find the number of terms, which represents the number of rungs here.
Next, we will find the sum of all the length of all the rungs by the formula:
So the total length of the wood required for all the rungs will be 385 cm.
Note: It can be noted that the sum of n terms of the AP can be found using the formula:
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




