Question

A ladder leaning against a wall makes an angle of \[{{60}^{\circ }}\] with the horizontal. If the fact of the ladder is 2.5 m away from the wall, find the length of the ladder.

Answer 1

- Hint:- Draw figure as per mentioned in the question. Consider the triangle formed. Take the cosine function and find the length of the ladder.

Complete step-by-step answer: -

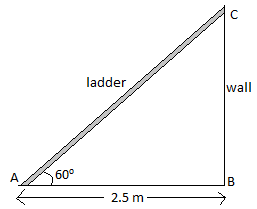
From the figure you can understand that BC is the wall in which the ladder AC is leaning against.
It is said that the ladder AC makes \[{{60}^{\circ }}\] angle with the horizontal, i.e. the ladder is leaning against the wall at an angle of \[{{60}^{\circ }}\].
Now the distance between the foot of the ladder and the wall is 2.5 m. Thus from the figure, you can say that, AB = 2.5 m.
Now the wall is perpendicular to the ground. So BC is perpendicular to AB, i.e. \[BC\bot AB\] and \[\angle ABC={{90}^{\circ }}\].
Now let us consider \[\Delta ABC\], from the figure.
\[\begin{align}
  & \cos {{60}^{\circ }}=\dfrac{adjacent\text{ }angle}{hypotenuse}=\dfrac{AB}{AC} \\
 & \cos {{60}^{\circ }}=\dfrac{2.5}{AC} \\
 & \Rightarrow AC=\dfrac{2.5}{\cos {{60}^{\circ }}} \\
\end{align}\]
From trigonometry, we know that \[\cos {{60}^{\circ }}={}^{1}/{}_{2}\].
\[\therefore AC=\dfrac{2.5}{{}^{1}/{}_{2}}=2.5\times 2=5\] m.
Thus we got AC = 5 cm.
So the length of the ladder is 5 cm.

Note:
We can find the length of the wall BC, by using Pythagoras theorem.
\[\begin{align}
  & A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} \\
 & B{{C}^{2}}=A{{C}^{2}}-A{{B}^{2}} \\
 & \Rightarrow BC=\sqrt{A{{C}^{2}}-A{{B}^{2}}}=\sqrt{{{5}^{2}}-{{\left( 2.5 \right)}^{2}}}=\sqrt{25-6.25}=\sqrt{18.75} \\
 & =4.33m \\
\end{align}\]
Thus, the height of the wall is 4.33 m.