Question

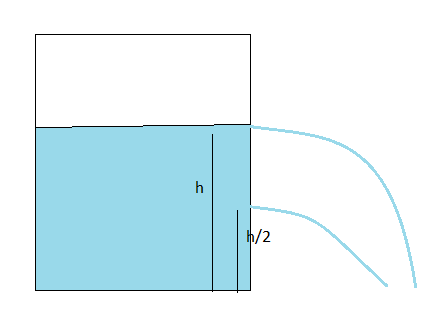
A large tank filled with water to a height $h$ is to be emptied through a small hole at the bottom. The ratio of time taken for the level of water to fall from $h$ to $\dfrac{h}{2}$ and from $\dfrac{h}{2}$ to $0$ is
A.$\sqrt 2 $
B.$\dfrac{1}{{\sqrt 2 }}$
C.$\sqrt 2 - 1$
D.$\dfrac{1}{{\sqrt 2 - 1}}$

Answer 1

Hint: Torricelli’s theorem states that the velocity v of a fluid flowing through a small hole at the bottom of a tank filled to a depth will have the same speed just like a body falling freely from a height $h$.
Using Torricelli’s theorem we can derive the relation for time and height and in general, for a cylindrical container, time to empty a tank is directly proportional to the difference of square root of initial height and the square root of final height.
Formula Used:
The ratio of time taken for the level of water to fall from a height $h$ to $\dfrac{h}{2}$ and from $\dfrac{h}{2}$ to $0$
 is given as
$\dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{\sqrt h - \sqrt {\dfrac{h}{2}} }}{{\sqrt {\dfrac{h}{2}} }} \ldots ..\left( {\because t \propto \sqrt {{h_1}} - \sqrt {{h_2}} } \right)$

Complete answer:
Given that,
Case I:
Initial height, \[{h_1} = {\text{ }}h\]
Final height, \[{h_2} = \dfrac{h}{2}\]
Case II:
Initial height, \[h{'_1} = \dfrac{h}{2}\]
Final height, \[h{'_2} = {\text{ }}0\]
Now according to Torricelli’s theorem, the velocity of water through a small hole is given as
$v = \sqrt {2gh} $
$\therefore \dfrac{{dh}}{{dt}} = \sqrt {2gh} $
By integrating this we get
$t = \mathop \smallint \nolimits_0^h \dfrac{{dh}}{{\sqrt {2gh} }}$
$t\; = \;\sqrt {\dfrac{{2h}}{g}} $
This equation represents the time of flight.
Using this we can derive the relation for the level of water to fall from height $\dfrac{h}{2}$ to $0$
i.e., ${t_1} = \sqrt {\dfrac{2}{g}} \left( {\sqrt {\left( {{h_1}} \right)} - \sqrt {\left( {{h_2}} \right)} \;} \right) = \sqrt {\dfrac{2}{g}} \left( {\sqrt {\left( h \right)} - \sqrt {\left( {\dfrac{h}{2}} \right)} \;} \right)$…… (1)
Similarly, for case II, we get
${t_2} = \sqrt {\dfrac{2}{g}} \left( {\sqrt {\left( {h{'_1}} \right)} - \sqrt {\left( {h{'_2}} \right)} \;} \right) = \sqrt {\dfrac{2}{g}} \left( {\sqrt {\left( {\dfrac{h}{2}} \right)} - \sqrt {\left( 0 \right)} \;} \right)$……(2)
By dividing equations 1 and 2 we get

$\dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{\sqrt {\dfrac{2}{g}} \left( {\sqrt {\left( h \right)} - \sqrt {\left( {\dfrac{h}{2}} \right)} \;} \right){\text{}}}}{{\sqrt {\dfrac{2}{g}} \left( {\sqrt {\left( {\dfrac{h}{2}} \right)} \;} \right)}} = \dfrac{{\sqrt 1 - \sqrt {\left( {\dfrac{1}{2}} \right)} }}{{\sqrt {\left( {\dfrac{1}{2}} \right)} }}$
$\dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{\left( {\dfrac{{\sqrt 2 - 1}}{{\sqrt 2 }}} \right)}}{{1/\sqrt 2 }} = \sqrt 2 - 1$

Therefore, Option (C) is correct.

Note:
For this problem, we must note that Torricelli’s theorem and Bernoulli’s principle are only applicable for incompressible and non-viscous fluids like water.
Torricelli’s theorem is a special case of Bernoulli’s principle which states that the sum of kinetic energy, pressure energy, and potential energy per unit volume of an incompressible, non-viscous fluid moving in a streamlined irrotational flow will remain constant along a streamline.