
A layer of ice of thickness y is on the surface of a lake. The air is at constant temperature
Where k is the thermal conductivity of the ice,
Answer
482.1k+ views
Hint: As in the question thickness of layer of ice is given and also air at constant temperature and ice water interface is also given. Temperature of water is more than the ice, so heat will be there that is going from water to air through ice. By considering this, we can easily find the rate at which the thickness will be increased.
Complete step by step solution:
Consider one lake and it is having a layer of ice on its surface as shown. The thickness of the ice is y and the air is at constant temperature
Rate at which the thickness increases,
Where k is the thermal conductivity of the ice,
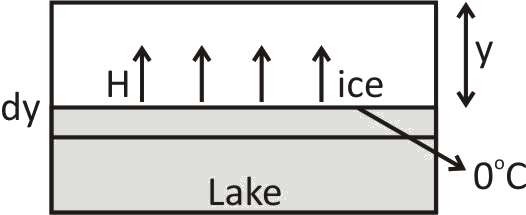
As heat will be going from water to air through ice, so
We know,
Compare equation (1) and (2), we get-
Also,
Here t is thickness, A is area and K is thermal conductivity.
Substitute the value of R in equation (3), we get-
This
If Q heat is used then,
Here L is the latent heat of the fusion.
We know,
So,
So, this is true.
Note:
The latent heat of fusion is the amount of heat that is gained by solid substance to convert into liquid without any other increase in temperature.
Or we can also solve directly by rate of loss of heat =
By comparing equations, we will get the
Complete step by step solution:
Consider one lake and it is having a layer of ice on its surface as shown. The thickness of the ice is y and the air is at constant temperature
Rate at which the thickness increases,
Where k is the thermal conductivity of the ice,

As heat will be going from water to air through ice, so
We know,
Compare equation (1) and (2), we get-
Also,
Here t is thickness, A is area and K is thermal conductivity.
Substitute the value of R in equation (3), we get-
This
If Q heat is used then,
Here L is the latent heat of the fusion.
We know,
So,
So, this is true.
Note:
The latent heat of fusion is the amount of heat that is gained by solid substance to convert into liquid without any other increase in temperature.
Or we can also solve directly by rate of loss of heat =
By comparing equations, we will get the
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




