Question

A legendary Dutch boy saved Holland by plugging a hole of diameter \[1.20cm\] in a dike with his finger. If the hole was $2.00m$ below the surface of the North Sea ( $density = 1030Kg{m^{ - 3}}$ ).
If he pulled his finger out of the hole, during what time interval would the release water fill $1$ acre of land to a depth of $1ft$ ? Assume the hole remained of land to a depth of $1ft$ ?Assume the hole remained constant in size.

Answer 1

Hint : In order to solve this equation, we will use the concept of Bernoulli theorem of fluid mechanics which states that “the sum of the pressure energy, Kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow always remains a constant”.

Complete step-by-step solution:
Let us first draw the diagram. Let $h$ be the height from top surface at which Dutch boy plugged a hole of given diameter $d = 1.2cm$ or $r = 0.06m$ where $r$ is the radius of the hole. And let $(1)$ denote the point where hole is made and $(2)$ is the point at the topmost surface.

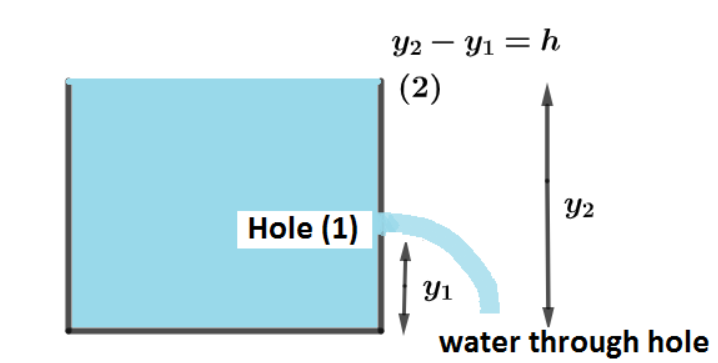
Now, we have
$\rho = 1030Kg{m^{ - 3}}$
${y_2} - {y_1} = h = 2m$
Let ${P_0}$ be the pressure at both points which are at top and at hole.
Then by using Bernoulli theorem we can write as:
${P_0} + \rho g{y_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_0} + \rho g{y_2} + 0$
Where ${v_1}$ is the velocity at hole.
$\dfrac{1}{2}\rho {v_1}^2 = \rho g{y_2} - \rho g{y_1}$
Or
${v_1} = \sqrt {2g({y_2} - {y_1})} $
Put ${y_2} - {y_1} = h = 2m$ in above equation we get,
${v_1} = \sqrt {2gh} $
On putting the values of $g = 9.8m{\sec ^{ - 2}}$ and $h = 2m$ we get,
${v_1} = \sqrt {4 \times 9.8} $
${v_1} = 6.26m{\sec ^{ - 1}}$
Now, Let $R$ denotes for the rate of the fluid and it’s calculated as $R = {A_1}{v_1}$ where ${v_1} = 6.26m{\sec ^{ - 1}}$ and ${A_1} = \pi {(0.06)^2}{m^2}$ be the area of the hole so,
$R = 6.26 \times 3.14 \times (0.0036)$
$R = 7.09 \times {10^{ - 4}}{m^3}{\sec ^{ - 1}}$
Now, as we know that volume of $1acreft = 1.236 \times {10^3}{m^3}$
So, in order to find time we can simple use $R = \dfrac{V}{t}$ where $R = 7.09 \times {10^{ - 4}}{m^3}{\sec ^{ - 1}}$ and $V = 1.236 \times {10^3}{m^3}$ on putting these values we get,
$t = \dfrac{{1.236 \times {{10}^3}{m^3}}}{{7.09 \times {{10}^{ - 4}}{m^3}{{\sec }^{ - 1}}}}$
Or
$t = 1.74 \times {10^6}\sec $
Hence, $1acreft = 1.236 \times {10^3}{m^3}$ of volume will be filled in $t = 1.74 \times {10^6}\sec $ .

Note: It should be remembered that, the basic units of conversions are as $1cm = 0.01m$ and the velocity of fluid at topmost point is zero because no water flows through this point and remember to notice the height $h$ as the difference in distances from ground level to topmost point and the distance from ground level to the point where hole is made.