Question

A light string is tied at one end to a fixed support and to a heavy of equal length L at the other end as shown in figure. A block of mass m is tied to the free and if heavy string, mass per unit length of the string S are $\mu $ and $9\mu $ and the tension is T. The ratio of number of loops n, $($in string of mass per unit length $\mu )$ and ${n_2}$ $($ In string of mass per unit length $9\mu )$ such that junction of 2 wire point A is a node

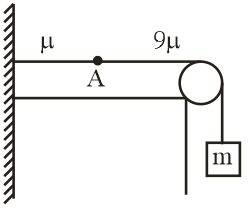
A. $1:2$
B. $1:3$
C. $1:4$
D. $1:9$

Answer 1

Hint: In order to solve above problem, first use the formula of number of loops in string which is
$\dfrac{{n\lambda }}{2} = L$
$n = \dfrac{{2L}}{\lambda }$ …..(1)
After then put the formula of wavelength $\lambda $
$v = f\lambda $
$\lambda = \dfrac{v}{f}$
Where
f $ = $ Frequency of wave
v $ = $ velocity of wave
Now, put the value of $\lambda $ in equation 1. We will get a number of loops in terms of velocity of waves.
So, $n = \dfrac{{2Lf}}{v}$
Now, using above formula compare number of lops for light string and heavy string and also put the formula of velocity of string i.e., $v = \sqrt {\dfrac{T}{\mu }} $
Where
$\mu = $ mass per unit length
$T = $Tension of string.

Complete step by step answer:
Given that the length of heavy string and light string is L. So, the formula for length of string in terms of number of loops is
$L = \dfrac{{n\lambda }}{2}$
So, for light string $L = \dfrac{{{n_1}{\lambda _1}}}{2}$ …..(1)
For heavy string $L = \dfrac{{{n_2}{\lambda _3}}}{2}$ …..(2)
We know that frequency is given as
$f = \dfrac{v}{\lambda }$
So, from equation 1 and 2
$f = \dfrac{{{v_1}}}{{{\lambda _1}}} = \dfrac{{{v_1}{n_1}}}{{2L}}$ …..(3)
$f = \dfrac{{{v_2}}}{{{\lambda _2}}} = \dfrac{{{v_2}{n_2}}}{{2L}}$ …..(4)
So, from equation 3 and 4
${v_1}{n_1} = {v_2}{n_2}$ …..(5)
Velocity of string in terms of tension and mass per unit length is
$v = \sqrt {\dfrac{I}{\mu }} $
So, ${v_1} = \sqrt {\dfrac{I}{{{\mu _1}}}} $ $[$Tension in one string is same$]$
${v_2} = \sqrt {\dfrac{T}{{{\mu _2}}}} $ …..(6)
From equation 5 and 6
$\sqrt {\dfrac{T}{{{\mu _1}}}} {n_1} = \sqrt {\dfrac{T}{{{\mu _2}}}} {n_2}$
$\dfrac{{{n_1}}}{{{n_\theta }}} = \sqrt {\dfrac{{{\mu _1}}}{{{\mu _2}}}} $
Here ${\mu _1}$ and ${\mu _2}$ are mass per unit length for light string and heavy string and given as
${\mu _1} = \mu $
${\mu _2} = 9\mu $
So, $\dfrac{{{n_1}}}{{{n_2}}} = \sqrt {\dfrac{\mu }{{9\mu }}} = \sqrt {\dfrac{1}{\delta }} $
$\implies \dfrac{{{n_1}}}{{{n_2}}} = \dfrac{1}{3}$
$\therefore {n_1}:{n_2} = 1:3$.

So, the correct answer is “Option B”.

Note:
Many times students may get confused in the concept of frequency when the medium is different. So, always remember that
When the medium is different but wave is same then frequency of wave does not change but its velocity and wavelength changes.