Question

A line DE is drawn parallel to base BC of $\triangle ABC$, meeting AB in D and AC in at E. If $\dfrac{{AB}}{{BD}} = 4$ and \[CE = {\text{ }}2{\text{ }}cm\], find the length of AE.

Answer 1

Hint:
In this question, we need to determine the length of the side AE such that DE is drawn parallel to the side BC in the triangle ABC. For this, we will first establish the relationship between the similar triangles and then substitute the values given in the question.

Complete step by step solution:
When DE is drawn parallel to BC then, it will form two triangles namely, ABC and ADE. Following is the pictorial representation of the same.

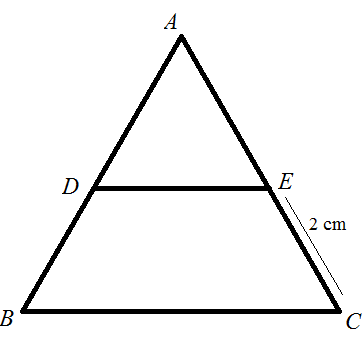
From the above figure, in the triangles ABC and ABD,
$\angle ADE = \angle ABC$, alternating angles of the parallel sides are equal.
Similarly, $\angle AED = \angle ACB$.
Hence, by AA similarity postulate, we can say that the triangles ABC and ADE are similar to one other.
Mathematically, $\vartriangle ABC \sim \vartriangle ADE$.
If the triangles are similar then, the sides of both the triangles are in proportion. So, here
$\dfrac{{AB}}{{AD}} = \dfrac{{AC}}{{AE}} = \dfrac{{DE}}{{BC}}$.
Here, we are continuing with only the first two terms, i.e., $\dfrac{{AB}}{{AD}} = \dfrac{{AC}}{{AE}} - - - - (i)$
Equation (i) can also be written by reciprocating the terms as:
$\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} - - - - (ii)$
Now, equation (ii) can also be re-written as:
$
1 - \dfrac{{AD}}{{AB}} = 1 - \dfrac{{AE}}{{AC}} \\
 \Rightarrow \dfrac{{AB - AD}}{{AB}} = \dfrac{{AC - AE}}{{AC}} - - - - (iii) \\
 $
As, $ AB-AD=BD $ and $ AC-AE=CE $ so, substituting these values in the equation (iii)

$
 \dfrac{{AB - AD}}{{AB}} = \dfrac{{AC - AE}}{{AC}} \\
  \Rightarrow \dfrac{{BD}}{{AB}} = \dfrac{{CE}}{{AC}} - - - - (iv) \\
 $
Now, it is given that $\dfrac{{AB}}{{BD}} = 4$ or, $\dfrac{{BD}}{{AB}} = \dfrac{1}{4}$ and $CE = 2$. So substituting these values in the equation (iv), we get
$
 \dfrac{{BD}}{{AB}} = \dfrac{{CE}}{{AC}} \\
 \Rightarrow \dfrac{1}{4} = \dfrac{2}{{AC}} \\
 AC = 8{\text{ cm}} - - - - (v) \\
 $
Now, from the figure, we can see that the summation of AE and EC is equals to AC. So, mathematically we can write
$
  AE + EC = AC \\
 \Rightarrow AE = AC - EC - - - - - (vi) \\
 $
Substituting the values from equation (v) in the equation (vi), we have the value of $AC = 8cm$ and $EC = 2cm$
$
  AE = AC - EC \\
   = 8 - 2 \\
   = 6{\text{ cm}} \\
 $
Hence, $AE = 6cm$

Note:
Students must be careful while writing the nomenclature of similar triangles. For, $\vartriangle ABC \sim \vartriangle ADE$ then, $\dfrac{{AB}}{{AD}} = \dfrac{{AC}}{{AE}} = \dfrac{{DE}}{{BC}}$. Here we can see that the positions of the letters (vertex) in the nomenclature of the triangles are strictly followed while writing the ratios of the sides.