
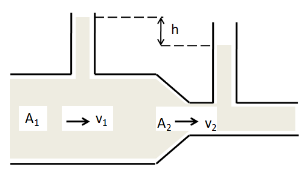
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquids in the two sections, which have areas of cross-section $ {A_1} $ and $ {A_2} $ , are $ {v_1} $ and $ {v_2} $ , respectively. The difference in the levels of the liquid in the two vertical tubes is $ h $ . Then
(A) $ {v_2}^2 - {v_1}^2 = 2gh $
(B) $ {v_2}^2 + {v_1}^2 = 2gh $
(C) $ {v_2}^2 - {v_1}^2 = gh $
(D) $ {v_2}^2 + {v_1}^2 = gh $

Answer
461.4k+ views
Hint: To solve this question we need to apply the Bernoulli’s equation at the two sections of the tube. On manipulating the equation obtained and setting the values given in the question, we will get the required relation.
Formula used: The formula which is used to solve this question is given by
$ P + \dfrac{{\rho {v^2}}}{2} + \rho gH = {\text{Constant}} $
Here $ P $ , $ v $ , and $ H $ are respectively the pressure, the velocity and the height above that of a fluid of density $ \rho $ .
Complete step by step solution:
Let the density of the liquid present in the horizontal tube be $ \rho $ .
The Bernoulli’s equation is given in the form,
$ \Rightarrow P + \dfrac{{\rho {v^2}}}{2} + \rho gH = {\text{Constant}} $
On applying this equation at the two sections of the horizontal pipe given in the question, we have
$ \Rightarrow {P_1} + \dfrac{{\rho {v_1}^2}}{2} + \rho g{H_1} = {P_2} + \dfrac{{\rho {v_2}^2}}{2} + \rho g{H_2} $
As the pipe is horizontal, so we have $ {H_1} = {H_2} $ . So putting this in the above equation, we get
$ \Rightarrow {P_1} + \dfrac{{\rho {v_1}^2}}{2} + \rho g{H_1} = {P_2} + \dfrac{{\rho {v_2}^2}}{2} + \rho g{H_1} $
Cancelling $ \rho g{H_1} $ from both the sides we get
$ \Rightarrow {P_1} + \dfrac{{\rho {v_1}^2}}{2} = {P_2} + \dfrac{{\rho {v_2}^2}}{2} $
On rearranging by taking the similar terms to one side, we have
$ \Rightarrow {P_1} - {P_2} = \dfrac{{\rho {v_2}^2}}{2} - \dfrac{{\rho {v_1}^2}}{2} $
$ \Rightarrow \Delta P = \dfrac{{\rho \left( {{v_2}^2 - {v_1}^2} \right)}}{2} $
From the figure given in the question, the liquid level of the first section is higher than that of the second section by $ h $ . So we have $ \Delta P = \rho gh $ . Substituting this in the above equation, we get
$ \Rightarrow \rho gh = \dfrac{{\rho \left( {{v_2}^2 - {v_1}^2} \right)}}{2} $
Cancelling $ \rho $ from both the sides we have
$ \Rightarrow gh = \dfrac{{\left( {{v_2}^2 - {v_1}^2} \right)}}{2} $
Multiplying by $ 2 $ both the sides, we finally get
$ {\Rightarrow v_2}^2 - {v_1}^2 = 2gh $
Hence, the correct answer is option (A).
Note:
We should not be confused between the height of the section of the pipe, and the level of the liquid present in the pipe. Although they both have the same dimensions, that is the length, but they both are different. The former indicates the potential energy of the fluid, while the latter indicates the pressure of the fluid.
Formula used: The formula which is used to solve this question is given by
$ P + \dfrac{{\rho {v^2}}}{2} + \rho gH = {\text{Constant}} $
Here $ P $ , $ v $ , and $ H $ are respectively the pressure, the velocity and the height above that of a fluid of density $ \rho $ .
Complete step by step solution:
Let the density of the liquid present in the horizontal tube be $ \rho $ .
The Bernoulli’s equation is given in the form,
$ \Rightarrow P + \dfrac{{\rho {v^2}}}{2} + \rho gH = {\text{Constant}} $
On applying this equation at the two sections of the horizontal pipe given in the question, we have
$ \Rightarrow {P_1} + \dfrac{{\rho {v_1}^2}}{2} + \rho g{H_1} = {P_2} + \dfrac{{\rho {v_2}^2}}{2} + \rho g{H_2} $
As the pipe is horizontal, so we have $ {H_1} = {H_2} $ . So putting this in the above equation, we get
$ \Rightarrow {P_1} + \dfrac{{\rho {v_1}^2}}{2} + \rho g{H_1} = {P_2} + \dfrac{{\rho {v_2}^2}}{2} + \rho g{H_1} $
Cancelling $ \rho g{H_1} $ from both the sides we get
$ \Rightarrow {P_1} + \dfrac{{\rho {v_1}^2}}{2} = {P_2} + \dfrac{{\rho {v_2}^2}}{2} $
On rearranging by taking the similar terms to one side, we have
$ \Rightarrow {P_1} - {P_2} = \dfrac{{\rho {v_2}^2}}{2} - \dfrac{{\rho {v_1}^2}}{2} $
$ \Rightarrow \Delta P = \dfrac{{\rho \left( {{v_2}^2 - {v_1}^2} \right)}}{2} $
From the figure given in the question, the liquid level of the first section is higher than that of the second section by $ h $ . So we have $ \Delta P = \rho gh $ . Substituting this in the above equation, we get
$ \Rightarrow \rho gh = \dfrac{{\rho \left( {{v_2}^2 - {v_1}^2} \right)}}{2} $
Cancelling $ \rho $ from both the sides we have
$ \Rightarrow gh = \dfrac{{\left( {{v_2}^2 - {v_1}^2} \right)}}{2} $
Multiplying by $ 2 $ both the sides, we finally get
$ {\Rightarrow v_2}^2 - {v_1}^2 = 2gh $
Hence, the correct answer is option (A).
Note:
We should not be confused between the height of the section of the pipe, and the level of the liquid present in the pipe. Although they both have the same dimensions, that is the length, but they both are different. The former indicates the potential energy of the fluid, while the latter indicates the pressure of the fluid.
Recently Updated Pages
Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

In case of conflict between fundamental rights of citizens class 7 social science CBSE

Can anyone list 10 advantages and disadvantages of friction

Trending doubts
10 examples of friction in our daily life

The correct order of melting point of 14th group elements class 11 chemistry CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is the specific heat capacity of ice water and class 11 physics CBSE

State and prove Bernoullis theorem class 11 physics CBSE




