
A long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
(A). 1.2
(B). 0.1
(C). 2.0
(D). 0.4
Answer
512.1k+ views
Hint: It is better to remember the whirl formation in the bucket of water when we are moving the water with our hand. Like this, if we are rotating a cylindrical vessel about its axis, the liquid will form a parabolic shape. According to this shape, the water has a larger height near to the surface of the vessel and shorter height nearly zero at the centre of the vessel. By balancing the forces acting on the water, we can find out the parabolic equation. With this parabolic equation, we can find out the height difference between the centre and the sides.
Formula used:
Centrifugal force,
Weight of the body,
Angular velocity,
Complete step by step answer:
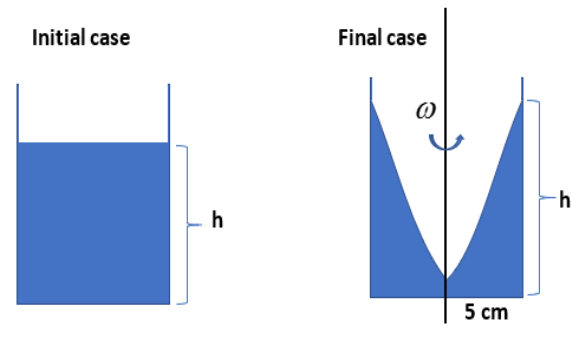
When we are rotating a cylinder with filled water, a force will arise and change the direction of water with its velocity. This force is known as the centrifugal force. This force will act towards the surface of the cylinder. As a result of this, the height of the water will change accordingly as shown in the figure. At the centre of the cylinder, the height of the water decreases and at the surfaces of the cylinder the height of water increases.
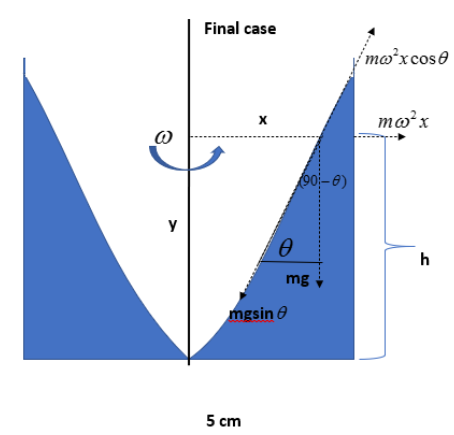
As shown in the figure, we have to consider a point at a distance x from the axis of rotation. In this figure, you can see the centrifugal force is acting towards the surface of the cylinder. Whereas, the weight of the liquid acting downwards.
Centrifugal force,
Weight of the body,
Here the water is rotating, so we have to consider the rectangular components of these forces. They will balance, hence the water won’t spill out.
Here we are dealing with the parabolic curve. So we can equate this with the parabolic equation.
We can see that the height of the water is varying with the position. So we can integrate this equation from 0 to h. The x is varying from 0 to r, where r is the radius of the cylinder.
In the question, we have already given the radius of the cylinder. Next, we have to find the angular velocity.
Now we can assign these values to the equation (1)
Note: You should remember to equate the equation that we generated from the force equilibrium to the equation of the parabola. Here the height is varying from 0 to h and x is varying from 0 to r. The weight and centrifugal forces are acting perpendicular. So we have to find out the rectangular components of these forces to find the equation of the parabola. Don’t forget to convert the units of radius and heights appropriately.
Formula used:
Centrifugal force,
Weight of the body,
Angular velocity,
Complete step by step answer:

When we are rotating a cylinder with filled water, a force will arise and change the direction of water with its velocity. This force is known as the centrifugal force. This force will act towards the surface of the cylinder. As a result of this, the height of the water will change accordingly as shown in the figure. At the centre of the cylinder, the height of the water decreases and at the surfaces of the cylinder the height of water increases.

As shown in the figure, we have to consider a point at a distance x from the axis of rotation. In this figure, you can see the centrifugal force is acting towards the surface of the cylinder. Whereas, the weight of the liquid acting downwards.
Centrifugal force,
Weight of the body,
Here the water is rotating, so we have to consider the rectangular components of these forces. They will balance, hence the water won’t spill out.
Here we are dealing with the parabolic curve. So we can equate this with the parabolic equation.
We can see that the height of the water is varying with the position. So we can integrate this equation from 0 to h. The x is varying from 0 to r, where r is the radius of the cylinder.
In the question, we have already given the radius of the cylinder. Next, we have to find the angular velocity.
Now we can assign these values to the equation (1)
Note: You should remember to equate the equation that we generated from the force equilibrium to the equation of the parabola. Here the height is varying from 0 to h and x is varying from 0 to r. The weight and centrifugal forces are acting perpendicular. So we have to find out the rectangular components of these forces to find the equation of the parabola. Don’t forget to convert the units of radius and heights appropriately.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




