Question

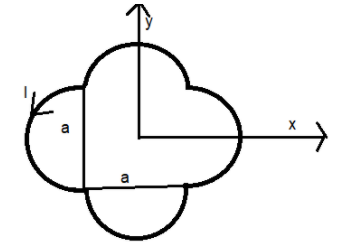
A loop carrying current I lies in the x-y plane as shown in the figure. The unit vector \[\widehat{k}\] is coming out of the plane of the paper. The magnetic moment of the current loop is?

\[\begin{align}
  & A)\text{ }{{\text{a}}^{2}}I\widehat{k} \\
 & B)\text{ (}\dfrac{\pi }{2}+1){{\text{a}}^{2}}I\widehat{k} \\
 & C)\text{ -(}\dfrac{\pi }{2}+1){{\text{a}}^{2}}I\widehat{k} \\
 & D)\text{ (2}\pi \text{-1)}{{\text{a}}^{2}}I\widehat{k} \\
\end{align}\]

Answer 1

Hint: The current carrying coil develops a magnetic field around the coil. The magnetic field is always perpendicular to the direction of current flow from the right-hand thumb rule. The area of the coil determines the magnetic field strength at a point.

Complete answer:
Let us consider the given coil as the source of the magnetic field. The magnetic moment is a quantity which determines the magnetic strength and its orientation with respect to the object that develops the magnetic field, here the coil. The magnetic moment is given by: \[\mu =N(I\times A)\], where N is the number of turns in the coil, I is the current through the coil and A is the area of the coil.
      

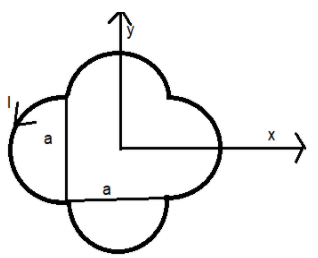
So, let us find the area of the given coil. It consists of four semicircles each of radius, \[r=\dfrac{a}{2}\] and a square of side a.
i.e., The area of the coil is given by,
\[\begin{align}
  & A=4\times \dfrac{\pi {{\left( \dfrac{a}{2} \right)}^{2}}}{2}+{{a}^{2}} \\
 & A=2\pi \dfrac{{{a}^{2}}}{4}+{{a}^{2}} \\
 & A={{a}^{2}}(\dfrac{\pi }{2}+1) \\
\end{align}\]
Now, let us find the magnetic moment of the coil,
\[\begin{align}
  & \mu =N(I\times A) \\
 & \mu =NIA\sin \theta \\
 & but\text{ }\theta ={{90}^{0}} \\
\end{align}\]
The current and area are perpendicular to each other,
So, \[\sin \theta =1\]
The magnetic moment is,
\[\begin{align}
  & \mu =NIA \\
 & \mu =1\times I{{a}^{2}}(\dfrac{\pi }{2}+1) \\
 & \therefore \mu =I{{a}^{2}}(\dfrac{\pi }{2}+1) \\
\end{align}\]
The direction of moment is perpendicular to both current and area, i.e., it is along \[\widehat{k}\]
Therefore, the magnetic moment is given by:
\[\mu \text{=(}\dfrac{\pi }{2}+1){{\text{a}}^{2}}I\widehat{k}\]

The correct answer is option B.

Note:
Magnetic dipole moment is the elaborated name given to the magnetic moments. In electrostatics, a pair of equal and opposite charges constitute a dipole, whereas in magnetostatics, there is no chance of monopoles. Magnetism is always dipole in nature.
The magnetic moment of an electron has a special unit known as Bohr Magneton (BM).