Question

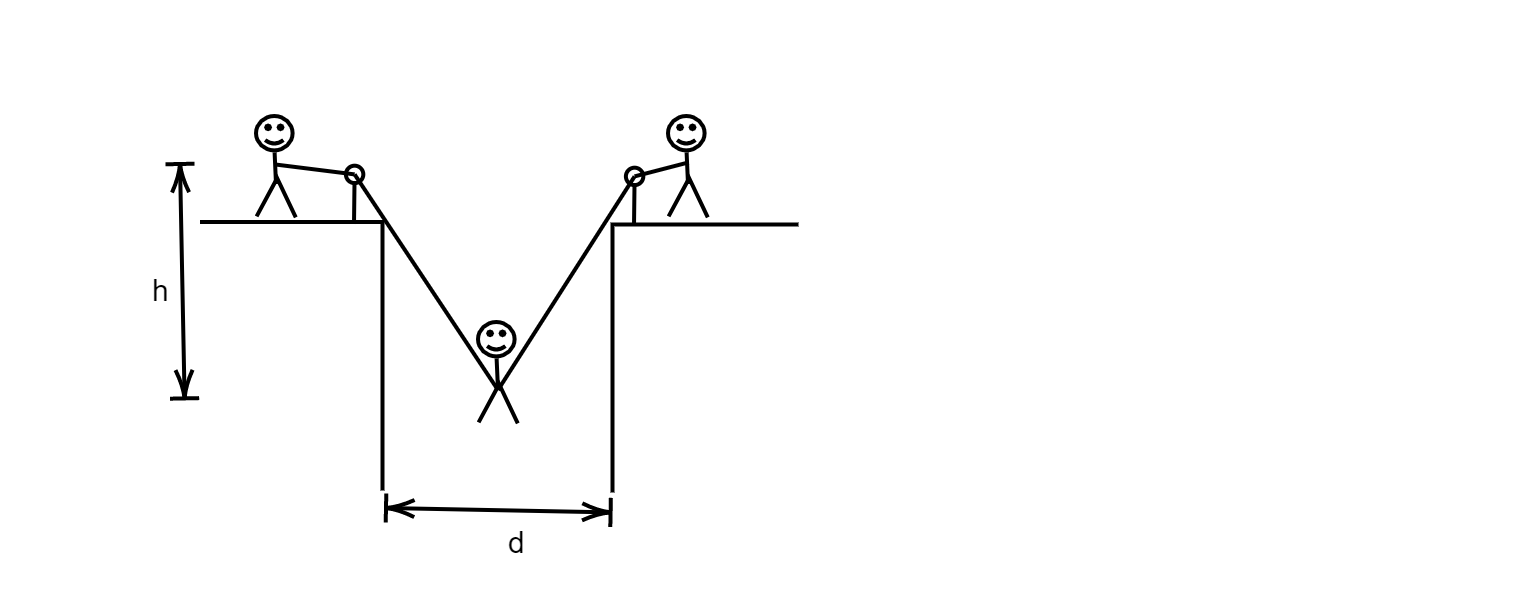
A man has fallen into a ditch of width $d$ and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in the figure. Show that the force (assumed equal for both the friends) exerted by each friend on the rope increases as the man moves up. Find the force when the man is at a depth $h$.

Answer 1

Hint: To solve these types of questions, our first step should be to make a detailed free body diagram so that we can figure out how the forces are acting on the system. Next step would be to form equations of forces and then solve them to get the required results.

Complete answer:
Let us first draw the free body diagram for better understanding and assume that the rope makes an angle $\theta $ with the vertical.

On observing the free body diagram, we can conclude that:
$\begin{align}
  & F\cos \theta +F\cos \theta =mg \\
 & \Rightarrow 2F\cos \theta =mg \\
 & \Rightarrow F=\dfrac{mg}{2\cos \theta } \\
\end{align}$
As the man’s friends pull him up, the angle that the rope makes with the vertical will increase and thus $\cos \theta $ will decrease.
We know that $\cos \theta $ is the length of the base of a right-angle triangle divided by the length of the hypotenuse, hence in this case we will consider the depth of the ditch as the base of the triangle and the length of the rope as the length of the hypotenuse, and hence we will get the following value:
\[\cos \theta =\dfrac{h}{\sqrt{\left( \dfrac{d}{2} \right)+{{h}^{2}}}}\]
Substituting this value in equation of force, we get:
\[\begin{align}
  & F=\dfrac{mg}{2\dfrac{h}{\sqrt{{{\left( \dfrac{d}{2} \right)}^{2}}+{{h}^{2}}}}} \\
 & \Rightarrow F=\dfrac{mg}{2\dfrac{h}{\sqrt{\dfrac{{{d}^{2}}+4{{h}^{2}}}{4}}}} \\
 & \Rightarrow F=\dfrac{mg}{4\dfrac{h}{\sqrt{{{d}^{2}}+4{{h}^{2}}}}} \\
 & \therefore F=\dfrac{mg}{4h}\sqrt{{{d}^{2}}+4{{h}^{2}}} \\
\end{align}\]
Hence, the force exerted by each of the friends increases as the man moves up.

Note:
An infinite amount of force would have to be applied to make the depth of the ditch zero, because force is inversely proportional to zero, hence if depth of the ditch decreases, i.e., as the man moves up, the force also increases and it would be practically impossible to make the horizontally straight by pulling the rope.