
A man is crossing a river flowing with velocity of
Answer
496.8k+ views
2 likes
Hint: Velocity of the river, width of the river and the time taken by man to cross the river is given and we have to find velocity of man in still water. Velocity is a vector quantity and it also gives direction. By using the formula of velocity and addition of vectors we can find the velocity of man in still water.
Formula used:
b>Complete answer:
A man was at point A of the river and crossed the river to reach at point B. The width of the river or the distance between A and B is 60m and the time taken to cross is 5 second.
As the river is flowing with velocity
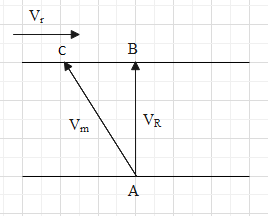
The velocity of river is
As velocity is a vector quantity because it gives us magnitude and direction, the above diagram can be given as
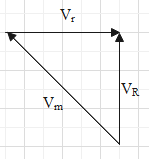
This is a vector diagram and from the addition of vectors we can write
Now the value of velocity of the river is given
Where S displacement and t is time. Here the width of river is the displacement i.e. 60m and time taken to cover it is 5 seconds, hence the resultant velocity is given as
Substituting the values of
Hence, the velocity of man is
So, the correct answer is “Option B”.
Note:
Distance and displacement has a slight difference, the distance just gives as magnitude but displacement gives us magnitude and direction as in the given question we have given the displacement when we consider the motion of the man as it tells us the direction in which he is moving which is from A to B.
Formula used:
b>Complete answer:
A man was at point A of the river and crossed the river to reach at point B. The width of the river or the distance between A and B is 60m and the time taken to cross is 5 second.
As the river is flowing with velocity

The velocity of river is
As velocity is a vector quantity because it gives us magnitude and direction, the above diagram can be given as

This is a vector diagram and from the addition of vectors we can write
Now the value of velocity of the river is given
Where S displacement and t is time. Here the width of river is the displacement i.e. 60m and time taken to cover it is 5 seconds, hence the resultant velocity is given as
Substituting the values of
Hence, the velocity of man is
So, the correct answer is “Option B”.
Note:
Distance and displacement has a slight difference, the distance just gives as magnitude but displacement gives us magnitude and direction as in the given question we have given the displacement when we consider the motion of the man as it tells us the direction in which he is moving which is from A to B.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




