Question

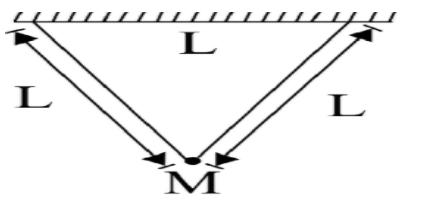
A man is swinging on a swing made of 2 ropes of equal length L and in direction perpendicular to the plane of paper. The time period of the small oscillations about the mean position is:

A. $2\pi \sqrt{L/2g}$
B. $2\pi \sqrt{\sqrt{3}L/2g}$
C. $2\pi \sqrt{L/2\sqrt{3}g}$
D. $\pi \sqrt{L/g}$

Answer 1

Hint: The motion of swing is similar to the motion of a simple pendulum. There is to and fro motion by which it repeats the same positions repeatedly. The time period is defined as the time needed to complete one oscillation, also it depends on the length of the pendulum.
Formula used:
The time period of oscillation is given by:
$T=2\pi \sqrt{L(eff.)/g}$

Complete answer:
The motion of the swing is the same as the motion of a simple pendulum, in which there is to and fro motion of oscillation.
Here, the swing is made of 2 equal lengths i.e. L.
In the simple pendulum, the mass m undergoes oscillations and it is suspended from a fixed rigid support in the gravitational force. When we pull the swing from an equilibrium position then it moves in vertical direction under the effect of gravity.
The motion of a simple pendulum executes simple harmonic motion (S.H.M) for small angles.
In the figure, AB is the effective length of the swing. The length of all of the sides is equal, forming an equilateral triangle which makes an angle of 60°.

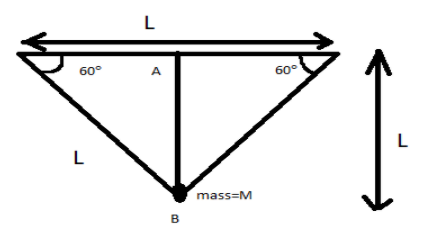
From the figure, we use Pythagoras theorem as,
$\begin{align}
  & \sin {{60}^{0}}=P/H \\
 & \sin {{60}^{0}}=AB/L \\
 & AB=\sqrt{3}L/2 \\
\end{align}$
The effective length as shown in figure is AB, and is calculated above.
Now we will discuss the time period of the oscillator as it is proportional to the square root of the length of the swing (or pendulum), and inversely proportional to the square root of the acceleration due to the gravity.
Now, we will calculate the time period of the oscillations:
$\begin{align}
  & T=2\pi \sqrt{L(eff.)/g} \\
 & \Rightarrow T=2\pi \sqrt{AB/g} \\
 & \Rightarrow T=2\pi \sqrt{\sqrt{3}L/g\times 2} \\
 & \Rightarrow T=2\pi \sqrt{\sqrt{3}L/2g} \\
\end{align}$

From the above calculations, we conclude that option B is the correct answer.

Note:
The motion of the swing is the same as the simple pendulum. It is given that the lengths of both the ropes are equal. The time period is directly proportional to the square of effective length and inversely to the acceleration due to gravity.