Question

A man on the top of a bamboo pole observes that the angle of depression of the base and the top of another pole is \[{60^ \circ }\,\&\, {30^ \circ }\] respectively. If the second pole stands \[5\]m above the ground level, then the height of the bamboo pole on which the man is sitting is:

Answer 1

Hint:As per the given information, we will draw the diagram. From the diagram we can equate the same length from there we can find the length of the required bamboo pole.

Formula used:
\[\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}\]
\[\tan {60^ \circ } = \sqrt 3 \]

Complete step-by-step answer:

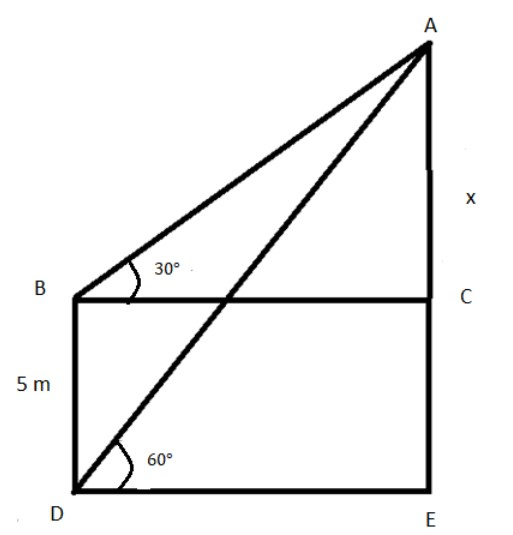
It is given that; a man on the top of a bamboo pole observes that the angle of depression of the base and the top of another pole is \[{60^ \circ }\,\&\, {30^ \circ }\] respectively. The length of the second pole is \[5\]m above the ground level.
We have to find the height of the bamboo pole on which the man is sitting.
As per the given problem, \[BD = 5\] and the angle of depression is given by \[\angle ABC = {30^ \circ }\,\&\, \angle ADE = {60^ \circ }\]
The man is sitting at the point A.
Let us consider, the length of \[AC\] be \[x\].
Since, \[BCED\] is a rectangle, the opposite sides are equal.
So, we have, \[BD = CE = 5\]
So, the length of the bamboo on which the man is sitting is \[AE = AC + CE\]
Now we find the length of \[AC.\]
From, \[\Delta ABC,\] we get,
\[ \Rightarrow \dfrac{{AC}}{{BC}} = \tan {30^ \circ }\]
Substitute the values we get,
\[ \Rightarrow \dfrac{x}{{BC}} = \dfrac{1}{{\sqrt 3 }}\]
Simplifying we get,
\[\therefore BC = x\sqrt 3 \]
From, \[\Delta ADE,\] we get,
\[ \Rightarrow \dfrac{{AE}}{{ED}} = \tan {60^ \circ }\]
Substitute the values we get,
\[ \Rightarrow \dfrac{{x + 5}}{{DE}} = \sqrt 3 \]
Simplifying we get,
\[\therefore DE = \dfrac{{x + 5}}{{\sqrt 3 }}\]
We already know that, \[DE = BC\]
Equating the length, we get,
\[ \Rightarrow x\sqrt 3 = \dfrac{{x + 5}}{{\sqrt 3 }}\]
Simplifying we get,
\[ \Rightarrow 3x = x + 5\]
Simplifying, again we get,
\[ \Rightarrow 2x = 5\]
\[\therefore x = \dfrac{5}{2} = 2.5\]
So, the length of the bamboo is \[AE = 5 + 2.5 = 7.5\]cm
Hence, the length of the bamboo is \[7.5\] cm.

Note:From the ratio between the angle and sides of a triangle we can form the equation.The downwards angle from the horizontal to a line of sight from the observer to some point of interest is known as the angle of depression.