
Answer
98.4k+ views
Hint: We can solve this question in two parts first we take lower medium after refraction the image formed will work as an object for upper medium then we take upper medium and find the apparent depth due to this medium that will be the final apparent depth.
Complete step by step solution:
In diagram the arrangement shown
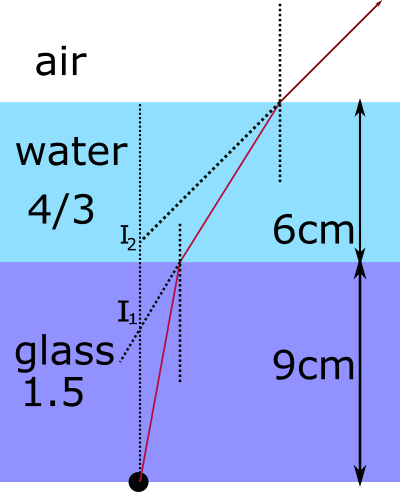
Step 1
First we take refraction from glass slab when see from water then apparent depth from upper end of glass slab can be calculated as
We know the apparent depth given by $AD = \dfrac{d}{{_r{n_d}}}$
Where $_r{n_d}$ is the refractive index of denser medium with respect to rare medium
$ \Rightarrow A{D_1} = \dfrac{9}{{_w{n_g}}}$
We know
$_w{n_g} = \dfrac{{_a{n_g}}}{{_a{n_w}}}$
So refractive index of glass with respect to water
$_w{n_g} = \dfrac{{\dfrac{3}{2}}}{{\dfrac{4}{3}}}$
$_w{n_g} = \dfrac{9}{8}$
So apparent depth
$ \Rightarrow A{D_1} = \dfrac{9}{{\dfrac{9}{8}}}$
$A{D_1} = 8cm$
Image formed at $8cm$ below upper end of glass slab this work as image for water
Step 2
Now we take refraction from water air surface
For this the real depth = height of water + AD1
Real depth = $\left( {6 + 8} \right) = 14cm$
Apply formula for apparent depth
$ \Rightarrow A{D_2} = \dfrac{{14}}{{_a{n_w}}}$
$ \Rightarrow A{D_1} = \dfrac{{14}}{{\dfrac{4}{3}}}$
Solving this
$ \Rightarrow A{D_2} = \dfrac{{21}}{2}cm$ from upper end of water surface
So the apparent depth due to system of both medium is $\left( {\dfrac{{21}}{2}} \right)cm$ when see from air
So the apparent depth of newspaper is $\left( {\dfrac{{21}}{2}} \right)cm.$
Note: By this method we can solve these types of questions we can also solve this question by another method:
We have direct formula for apparent depth if refractive index of medium ${n_1},{n_2}$ with respect to air and depth of medium is ${d_1},{d_2}$ then
$ \Rightarrow AD = \dfrac{{{d_1}}}{{{n_1}}} + \dfrac{{{d_2}}}{{{n_2}}}$
$ \Rightarrow AD = \dfrac{9}{{\dfrac{3}{2}}} + \dfrac{6}{{\dfrac{4}{3}}}$
Solving this
$
\Rightarrow AD = 6 + \dfrac{9}{2} \\
AD = \dfrac{{21}}{2}cm \\ $
Complete step by step solution:
In diagram the arrangement shown

Step 1
First we take refraction from glass slab when see from water then apparent depth from upper end of glass slab can be calculated as
We know the apparent depth given by $AD = \dfrac{d}{{_r{n_d}}}$
Where $_r{n_d}$ is the refractive index of denser medium with respect to rare medium
$ \Rightarrow A{D_1} = \dfrac{9}{{_w{n_g}}}$
We know
$_w{n_g} = \dfrac{{_a{n_g}}}{{_a{n_w}}}$
So refractive index of glass with respect to water
$_w{n_g} = \dfrac{{\dfrac{3}{2}}}{{\dfrac{4}{3}}}$
$_w{n_g} = \dfrac{9}{8}$
So apparent depth
$ \Rightarrow A{D_1} = \dfrac{9}{{\dfrac{9}{8}}}$
$A{D_1} = 8cm$
Image formed at $8cm$ below upper end of glass slab this work as image for water
Step 2
Now we take refraction from water air surface
For this the real depth = height of water + AD1
Real depth = $\left( {6 + 8} \right) = 14cm$
Apply formula for apparent depth
$ \Rightarrow A{D_2} = \dfrac{{14}}{{_a{n_w}}}$
$ \Rightarrow A{D_1} = \dfrac{{14}}{{\dfrac{4}{3}}}$
Solving this
$ \Rightarrow A{D_2} = \dfrac{{21}}{2}cm$ from upper end of water surface
So the apparent depth due to system of both medium is $\left( {\dfrac{{21}}{2}} \right)cm$ when see from air
So the apparent depth of newspaper is $\left( {\dfrac{{21}}{2}} \right)cm.$
Note: By this method we can solve these types of questions we can also solve this question by another method:
We have direct formula for apparent depth if refractive index of medium ${n_1},{n_2}$ with respect to air and depth of medium is ${d_1},{d_2}$ then
$ \Rightarrow AD = \dfrac{{{d_1}}}{{{n_1}}} + \dfrac{{{d_2}}}{{{n_2}}}$
$ \Rightarrow AD = \dfrac{9}{{\dfrac{3}{2}}} + \dfrac{6}{{\dfrac{4}{3}}}$
Solving this
$
\Rightarrow AD = 6 + \dfrac{9}{2} \\
AD = \dfrac{{21}}{2}cm \\ $
Recently Updated Pages
Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

Write an article on the need and importance of sports class 10 english JEE_Main

Name the scale on which the destructive energy of an class 11 physics JEE_Main

Choose the exact meaning of the given idiomphrase The class 9 english JEE_Main

Choose the one which best expresses the meaning of class 9 english JEE_Main




