Question

A man standing on a truck which moves with a constant horizontal acceleration $ 10m{\text{ }}{s^{ - 2}} $ when the speed of the truck is $ 10m{\text{ }}{s^{ - 1}} $ . The man throws a ball with velocity $ 5\sqrt 2 m{\text{ }}{s^{ - 1}} $ with respect to the truck. In the direction shown in the diagram. Find the displacement of the ball in metres in one second as observed by the man. ( $ g = 10m{\text{ }}{s^{ - 2}} $ )

Answer 1

Hint: To solve this question, we must have a concept of vector motion of the equation then we can easily solve this question. Here in this question, first we will write all the given content in vector form and then we will find the velocity of the ball with respect to the truck and then substituting all the required values in the second equation of motion and hence we got our required solution.
 $ s = {V_b}t + \dfrac{1}{2}a{t^2} $
 $ s $ is the displacement,
 $ V $ is the velocity,
 $ t $ is the time taken and
 $ a $ is the acceleration.

Complete Step By Step Answer:
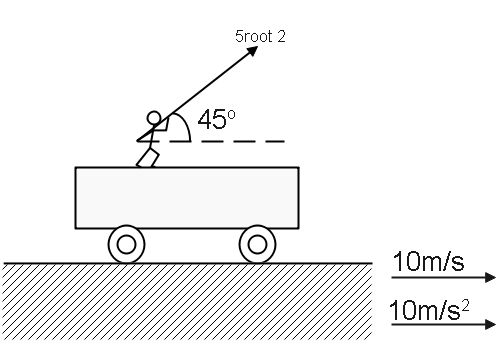
According to the question,
The speed of the truck is $ 10m{\text{ }}{s^{ - 1}} $ and
Also, it is given that the velocity of the ball with respect to the truck is $ 5\sqrt 2 m{\text{ }}{s^{ - 1}} $ .
Now, let us write in the vector form,
Velocity of the truck in vector form $ {V_t} = 10i $ and
The velocity of the ball with respect to the truck in vector form $ V(b,t) = {V_b} - {V_t} $
We can write the above equation as:
 $ 5\sqrt 2 (\cos {45^ \circ } + \sin {45^ \circ }) = {V_b} - {V_t} $
Where as the value of $ {V_t} = 10i $
Now simply substituting the value of $ {V_t} $
 $
  5\sqrt 2 (\cos {45^ \circ } + \sin {45^ \circ }) = {V_b} - 10i \\
   \Rightarrow {V_b} = 5i + 5j + 10i \\
   \Rightarrow {V_b} = 15i + 5j \\
  $
Now, we have the velocity of the ball i.e., $ {V_b} = 15i + 5j $ .
And as per the question, the acceleration of the truck with respect to ground is $ a = 10i + ( - g)j $
Or we can write, $ a = 10i - 10j $
Now applying second equation of motion, to find the displacement of the ball with respect to ground,
i.e., $ s = {V_b}t + \dfrac{1}{2}a{t^2} $
 $
  s = \left( {15i + 5j} \right) \cdot 1 + \dfrac{1}{2}\left( {10i - 10j} \right){1^2} \\
   \Rightarrow s = 15i + 5j + 5i - 5j \\
   \Rightarrow s = 20i \\
  $
So, the displacement of the ball with respect to the ground is $ 20i $ i.e., $ 20m $ .

Note:
Note that this question comes under relative motion and to solve these types of questions just analyse all the content with respect to ground and solve the obtained equation and after that find what is asked accordingly. Let’s say relative velocity of a car with respect to truck is nothing but the rate of change of position of car with respect to truck. And is given by, $ {V_{car,truck}} = {V_{car}} - {V_{truck}} $ .