Question

A massless conical flask filled with a liquid is kept on a table in a vacuum. The force exerted by the liquid on the base of the flask is ${{W}_{1}}$. The force exerted by the flask on the table is ${{W}_{2}}$ . (This question has multiple correct options)

A. ${{W}_{1}}={{W}_{2}}$
B. ${{W}_{1}}\rangle {{W}_{2}}$
C. ${{W}_{1}}\langle {{W}_{2}}$
D. The force exerted by the liquid on the walls of the flask is$\left( {{W}_{1}}-{{W}_{2}} \right)$ .

Answer 1

Hint: As a first step, you could go for finding the force exerted by the liquid on the walls of the given flask. We will then get the resultant of this force only in the upward direction as all its horizontal components on either side of the flask get cancelled. This force when subtracted from the force exerted by the liquid at the base will give you ${{W}_{2}}$ .

Complete step-by-step answer:
We are given a massless conical flask filled with a liquid. Also the force exerted by the liquid on the base of the flask is taken as ${{W}_{1}}$ and the force exerted by the flask on the table is taken as ${{W}_{2}}$. We are asked to find the relation between them.

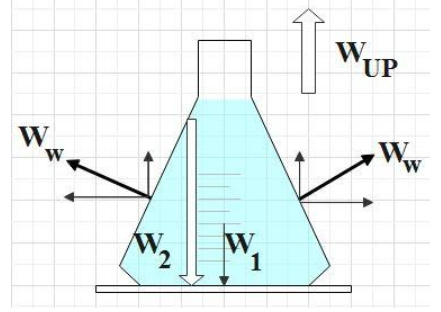
Recall that, by Pascal’s law, the pressure for a liquid at rest is the same at all points provided they are at the same height. So, there definitely exists a pressure that is exerted by the liquid at the walls of the conical flask. Let us consider a pressure exerted at corresponding points on either side of the conical flask and let us represent the force responsible for it by ${{W}_{W}}$. If we resolve this force into its components we get equal and opposite horizontal components on either side of the conical flask which cancels each other. So, all that remains of the force exerted by the liquid on the wall is its vertical component. Hence, we get net force ${{W}_{up}}$ directed upwards as the resultant of all the vertical components.
The force ${{W}_{2}}$ could be defined either as the force exerted by the flask on the table or as that exerted by table on the flask since both these forces should be equal for the conical flask to be at rest on the table. Logically, force exerted by the flask on the table should be the resultant of the forces exerted by liquid at the base of the flask and at its walls. That is,
${{W}_{2}}={{W}_{1}}-{{W}_{UP}}$ ………………… (1)
Since ${{W}_{2}}$ is given by ${{W}_{1}}$ minus some quantity$\left( {{W}_{UP}} \right)$,
${{W}_{2}}\langle {{W}_{1}}$ …………………….. (2)
Also, from (1) we have,
${{W}_{UP}}={{W}_{1}}-{{W}_{2}}$ ……………………. (3)
Where, ‘${{W}_{UP}}$’ is the resultant of all the forces exerted on the walls of the conical flask by the liquid.
Hence, the correct options for this question are option B and option D.

Note: If you are worried about not considering the atmospheric pressure that is exerted at the surface of the liquid, remember that the system under consideration is at vacuum which has no atmosphere. Also note that, we are also excluding weight (mg) of the conical flask exerted against gravity. This is because we are given a massless flask in the question, hence the weight is negligible.