Question

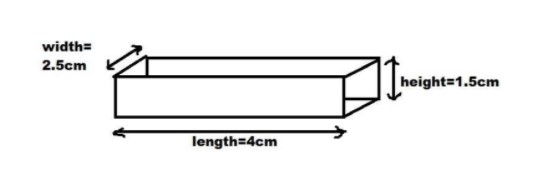
A matchbox is \[4cm\] long \[2.5cm\] broad and $1.5cm$ in height. Its outer sides are to be covered exactly with craft paper. How much paper will be required to do so?

Answer 1

Hint:Note down all the measurements perfectly. As we are asked to cover the outer surface exactly with the craft paper, we need to find out the outer surface area of the matchbox. It will be equal to the required amount of craft paper.


Complete step-by-step answer:
Let us initially note down the dimensions of the matchbox,
Length if the matchbox is \[4cm\].
Width of the matchbox is \[2.5cm\].
Height of the matchbox is $1.5cm$.
When we visualize the matchbox with the above given dimensions, it looks like a cuboid.

Now, we need to find out the craft paper required in order to exactly cover the total outer surface of the matchbox.
It means clearly, we can say that the amount of craft paper required is exactly equal to the outer surface of the cuboid.
Outer surface has six faces with three pairs.
So, we need to find out the area of three rectangles with different dimensions and twice that as there are three more similar rectangles present.
And we are well familiar with the formula of total surface area of the cuboid also.
Total surface area of the cuboid is $2\left( {lb + bh + hl} \right)$ in square units.
Where $l$ is the length of the cuboid, $b$ is the width of the cuboid and $h$ is the height of the cuboid.
As we already have the values of $l$, $b$ and $h$ as \[4cm\], \[2.5cm\] and \[1.5cm\] respectively. Substitute the values in the formula to get the required solution.
Hence, the outer surface area of the matchbox $ = 2\left( {lb + bh + hl} \right)$
                                      $
   = 2\left( {4 \times 2.5 + 2.5 \times 1.5 + 1.5 \times 4} \right) \\
   = 2\left( {10 + 3.75 + 6} \right) \\
   = 2\left( {19.75} \right) \\
   = 39.5c{m^2} \\
 $

Therefore, we need $39.5c{m^2}$ of craft paper to cover the matchbox exactly.

Note:Cuboid has 6 faces with three different rectangular faces.The area of craft paper to cover the cuboid (Match box) is total surface area of cuboid which is given by $ = 2\left( {lb + bh + hl} \right)$.Students should remember this formula for solving these types of questions.