Question

A metallic element crystallizes into a lattice containing a sequence of layers of ABABAB. Any packing of spheres leaves out voids in the lattice. What percentage by volume of this lattice is occupied by voids?

Answer 1

Hint:Predict the crystal lattice structure of the metallic element. Then calculate the void that will remain per unit cell of the crystal lattice, this will give you the volume occupied by voids.

Complete answer:
It is given as an ABABAB type of arrangement. We know that the ABABAB type is for HCP lattice which is hexagonal close packing. For hexagonal close packing, we know that there are 6 atoms per unit cell.

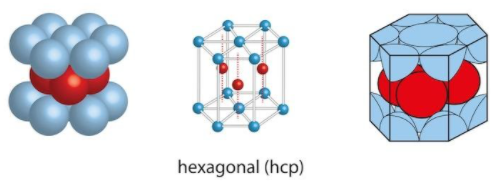
To find the packing fraction of the HCP lattice we can use the formula:
\[\text{Packing fraction = }\dfrac{\text{Volume occupied by atoms}}{\text{Volume of unit cell}}\times 100\]
The volume occupied by the metallic atoms if the radius is $r$is given by:
\[\text{Volume occupied by atoms = No}\text{.of atoms }\times \text{ volume of one sphere(atom)}\]
Thus, the equation will be:
\[\text{Volume occupied by atoms = 6}\times \dfrac{4}{3}\times \pi \times {{r}^{3}}\]
\[\text{Volume occupied by atoms = 25}\text{.073}{{r}^{3}}\]
The volume of the HCP crystal lattice unit will be:
\[\text{Volume of unit cell = Area of base }\times \text{ Height}\]
We know that the area of the base and the height of an HCP unit cell with respect to the radius of the atoms is:
Area of base = $6\sqrt{3}{{r}^{2}}$
Height of unit cell = $4r\times \sqrt{\dfrac{2}{3}}$
Thus, the volume of the unit cell is:
\[\text{Volume of unit cell = 6}\sqrt{3}{{r}^{2}}\times 4r\times \sqrt{\dfrac{2}{3}}\]
Calculating the volume, we get:
\[\text{Volume of unit cell = 6}\times 4\times \text{1}\text{.414}\times {{\text{r}}^{3}}\]
\[\text{Volume of unit cell = 33}\text{.936}{{r}^{3}}\]
Putting in formula to calculate packing fraction, we get:
\[\text{Packing fraction = }\dfrac{25.073{{r}^{3}}}{33.936{{r}^{3}}}\times 100\]
\[\text{Packing fraction = }73.88%\]
Therefore, the percentage void is equal to = $100-\text{packing fraction}$
\[\text{Percentage void = 100}-73.88\]
\[\text{Percentage void = }26.12%\]
So, 26.12% volume of this lattice is occupied by voids.

Additional Information:
We know that crystal lattice is made up of a very large number of unit cells in which every single lattice point is filled by one constituent particle. We can see the unit cells containing one or more atoms in a three-dimensional structure.
We can easily calculate the coordination number, area of the bae of the HCP lattice and also its height by doing some basic calculations using the definitions for the areas of basic geometric shapes like triangles.

Note:
You should notice that the hexagonal close packing (hcp) and the face centred cubic lattices have a similar way of arranging molecules. But in the face-centred, the layers are labelled as ABCABC. Three, different layers make up the lattice but the coordination number is 6.