Question

A milk container is made of metal sheet in the shape of frustum of a cone whose volume is $10459\dfrac{3}{7}c{{m}^{3}}$. The radii of its lower and upper circular ends are 8cm and 20cm respectively. Find the cost of the metal sheet used in making the container at the rate of $Rs.1.40\ per\ c{{m}^{3}}.\left( Use\ \pi =22.7 \right)$.

Answer 1

Hint: At first use the volume formula $\dfrac{\pi }{3}h\left( {{R}^{2}}+{{r}^{2}}+Rr \right)$ which is volume of frustum to get the value of ‘h’ or height. Now further use the data to get value of surface area using $\pi \left( R+r \right)\sqrt{{{\left( R-r \right)}^{2}}+{{h}^{2}}}+\pi {{R}^{2}}$ and then multiply with Rs.1.40 to find the cost.

Complete step-by-step answer:
In the question we are given a milk container which is in the shape of a frustum of a cone. We have to find the total surface area of the cone so as to get the cost of the metal sheet to cover the container.

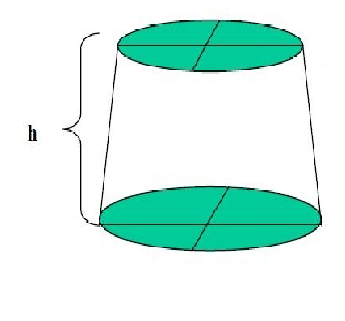
The data or the dimensions of the frustum of the cone given are radii of its lower and upper circular surfaces are 8cm and 20cm respectively. The volume is already given as $10459\dfrac{3}{7}c{{m}^{3}}$.

To find the surface area we are given the formula with opening on the smaller side of base ‘r’ of frustum,

$\pi \left( R+r \right)\sqrt{{{\left( R-r \right)}^{2}}+{{h}^{2}}}+\pi {{R}^{2}}$

Where R, r are the radius of larger and smaller circular bases respectively and h is height.
The formula of volume is,

$\dfrac{\pi }{3}h\left( {{R}^{2}}+{{r}^{2}}+Rr \right)$

Where R, r are the radius of larger and smaller circular bases respectively and h is height.

The volume given is $10459\dfrac{3}{7}c{{m}^{3}}$ which can be written as $\dfrac{73216}{7}c{{m}^{3}}$.

Now it can be written as,

$\dfrac{\pi }{3}h\left( {{R}^{2}}+{{r}^{2}}+Rr \right)=\dfrac{73216}{7}c{{m}^{3}}$

Here $\pi =\dfrac{22}{7},R=20,r=8$.

So,

$\dfrac{1}{3}\times \dfrac{22}{7}\times h\left( {{20}^{2}}+{{8}^{2}}+20\times 8 \right)=\dfrac{73216}{7}$

Which can be written as,

$h\left( {{20}^{2}}+{{8}^{2}}+160 \right)=\dfrac{73216}{7}\times \dfrac{21}{22}$

Which can be further solved as,

$h\left( 624 \right)=9984$

So,

$h=\dfrac{9984}{624}=16cm$

Hence the height of the frustum of the cone is 16cm.
Now, we have to get the value of surface area of frustum with an opening on the circular base of radius ‘r’,

$\pi \left( R+r \right)\sqrt{{{\left( R-r \right)}^{2}}+{{h}^{2}}}+\pi {{R}^{2}}$

Here $R=20,r=8,h=16\ \And \ \pi =\dfrac{22}{7}$

So, the surface area is,

$=\dfrac{22}{7}\times \left\{ \left( 20+8 \right)\sqrt{{{\left( 20-8 \right)}^{2}}+{{16}^{2}}}+{{20}^{2}} \right\}$

Which can be calculated as,

$\dfrac{22}{7}\times 28\times \sqrt{{{12}^{2}}+{{16}^{2}}}+\dfrac{22}{7}\times {{\left( 20 \right)}^{2}}$

By doing calculations carefully we can write it as,

$\begin{align}

  & \dfrac{22}{7}\times \left\{ 28\times \sqrt{400}+{{20}^{2}} \right\} \\

 & =\dfrac{22}{7}\times \left\{ 560+4 \right\}=\dfrac{21120}{7}c{{m}^{2}} \\

\end{align}$

Hence, the area of metal sheet required is $\dfrac{21120}{7}c{{m}^{2}}$

Now for the costing it was given that for $1c{{m}^{2}}$ of metal material Rs.1.40 is required.

So, the total cost is $Rs.\left( \dfrac{21120}{7}\times 1.40 \right)$ which is equal to Rs. 4224.

Hence the cost of metal sheet is Rs. 4224.


Note: Students might get confused in this problem whether to include $\pi {{r}^{2}}$ in the surface area and costing or not. They should not include it because in the question we are given to find the area of the container which is opened in the circular base with a smaller radius.