
A monocycle is a wheel with one wheel only. The monocycle has a symmetric wheel of mass m, radius R and moment of inertia I about its own axis. An engine given constant torque
Answer
495.9k+ views
Hint: It is given in the question that the wheel rotates on a sufficiently rough surface. Hence the frictional force by the ground will oppose the net torque by the engine. The frictional force acts as a tangential force opposite to the rotation of the wheel, hence it will also exert a torque as a result of which the monocycle will rotate with a net torque.
Formula used:
The above monocycle wheel has moments of inertia I and radius R. As the wheel rotates with a net torques it is equal to,
Complete answer:
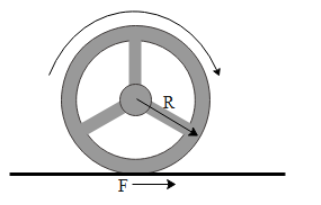
In the above diagram we can see that the monocycle rotates clockwise. Hence the friction force F acts towards the right. The wheel rotates due to the torque by the engine. Since the frictional force comes into action, the wheel will also translate along the horizontal right direction. Since force is given by mass times the linear acceleration, the acceleration (a) of the wheel along the centre of mass is,
The relation between the linear acceleration (a) and the angular acceleration
Equating equation 1 and 2, the net angular acceleration is given by,
The net torques on the monocycle is given by,
Substituting for angular acceleration in the above equation we get,
Hence the correct answer to the above question is option d.
Note:
It is to be noted that the frictional force is the force responsible for the translational motion of a circular object when rotating on ground. If there was no friction then the wheel would have rotated just there itself without moving forward. Hence the relative motion between the ground and the circular body is always zero.
Formula used:
The above monocycle wheel has moments of inertia I and radius R. As the wheel rotates with a net torques it is equal to,
Complete answer:

In the above diagram we can see that the monocycle rotates clockwise. Hence the friction force F acts towards the right. The wheel rotates due to the torque by the engine. Since the frictional force comes into action, the wheel will also translate along the horizontal right direction. Since force is given by mass times the linear acceleration, the acceleration (a) of the wheel along the centre of mass is,
The relation between the linear acceleration (a) and the angular acceleration
Equating equation 1 and 2, the net angular acceleration is given by,
The net torques on the monocycle is given by,
Substituting for angular acceleration in the above equation we get,
Hence the correct answer to the above question is option d.
Note:
It is to be noted that the frictional force is the force responsible for the translational motion of a circular object when rotating on ground. If there was no friction then the wheel would have rotated just there itself without moving forward. Hence the relative motion between the ground and the circular body is always zero.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




