Question

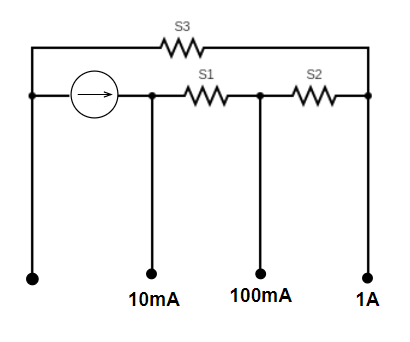
A multi-range current meter can be constructed by using a galvanometer circuit as shown in fig. We want a current meter that can measure 10mA, 100mA and 1A using a galvanometer of resistance $10\Omega $ and that produces maximum deflection for current of 1mA. Find ${{S}_{1}},{{S}_{2}},{{S}_{3}}$that have to be used.
                                        

Answer 1

Hint: In order to construct a multi-range current meter, we would first need to understand the direction of flow of these currents through their respective shunt resistance. We will first calculate the net shunt resistance of the circuit using its formula and this net shunt will be equal to the sum of all shunt resistance in the series.

Complete answer:
Let us first assign some terms that we are going to use later in our solution.
Let us the net shunt resistance of the circuit be ‘S’, such that:
$\Rightarrow S={{S}_{1}}+{{S}_{2}}+{{S}_{3}}$ [Let this expression be equation number (1)]
Also, let the galvanometer current be ${{I}_{G}}$. Then, it is given that:
$\Rightarrow {{I}_{G}}=1mA$
Now, in the first case:
$\Rightarrow I=10mA$
Therefore, we can write:
$\begin{align}
  & \Rightarrow S=\dfrac{{{I}_{G}}\times G}{I-{{I}_{G}}} \\
 & \Rightarrow S=\dfrac{1\times 10}{10-1}\Omega \\
 & \Rightarrow S=\dfrac{10}{9}\Omega \\
\end{align}$
Thus, putting this in equation (1), we get:
$\Rightarrow {{S}_{1}}+{{S}_{2}}+{{S}_{3}}=\dfrac{10}{9}\Omega $ [Let this expression be equation number (2)]
Now, in the second case (G to \[{{S}_{1}}\]), we have:
$\Rightarrow I=100mA$
$\Rightarrow G'=G+{{S}_{1}}$
And, $S={{S}_{2}}+{{S}_{3}}$
Therefore, we can write:
$\begin{align}
  & \Rightarrow \left( {{S}_{2}}+{{S}_{3}} \right)=\dfrac{\left( G+{{S}_{1}} \right)\times {{I}_{G}}}{I-{{I}_{G}}} \\
 & \Rightarrow \left( {{S}_{2}}+{{S}_{3}} \right)=\dfrac{\left( 10+{{S}_{1}} \right)\times 1}{99}\Omega \\
\end{align}$
$\Rightarrow \left( {{S}_{2}}+{{S}_{3}} \right)=\dfrac{\left( 10+{{S}_{1}} \right)}{99}\Omega $ [Let this expression be equation number (3)]
Now, in the third case (G to \[{{S}_{2}}\]), we have:
$\Rightarrow I=100mA$
$\Rightarrow G''=G+{{S}_{1}}+{{S}_{1}}$
And, $S''={{S}_{3}}$
Therefore, we can write:
$\begin{align}
  & \Rightarrow \left( {{S}_{3}} \right)=\dfrac{\left( G+{{S}_{1}}+{{S}_{2}} \right)\times {{I}_{G}}}{I-{{I}_{G}}} \\
 & \Rightarrow \left( {{S}_{3}} \right)=\dfrac{\left( 10+{{S}_{1}}+{{S}_{2}} \right)\times 1}{999}\Omega \\
\end{align}$
$\Rightarrow {{S}_{3}}=\dfrac{\left( 10+{{S}_{1}}+{{S}_{2}} \right)}{999}\Omega $ [Let this expression be equation number (4)]
Now, putting equation (3) in equation (2), we get:
$\begin{align}
  & \Rightarrow {{S}_{1}}+\dfrac{G+{{S}_{1}}}{99}=\dfrac{10}{9} \\
 & \therefore {{S}_{1}}=1\Omega \\
\end{align}$
Now, putting the value of ${{S}_{1}}$in equation (3), we get:
$\Rightarrow {{S}_{2}}+{{S}_{3}}=\dfrac{1}{9}\Omega $ [Let this expression be equation number (5)]
And, putting the value of ${{S}_{1}}$in equation (4), we get:
$\Rightarrow {{S}_{3}}-\dfrac{{{S}_{2}}}{999}=\dfrac{11}{999}$ [Let this expression be equation number (6)]
Solving equation number (5) and (6), we get:
$\begin{align}
  & \Rightarrow {{S}_{2}}=0.1\Omega \\
 & \Rightarrow {{S}_{3}}=0.011\Omega \\
\end{align}$
Hence, the value of ${{S}_{1}},{{S}_{2}}\text{ and }{{S}_{3}}$ comes out to be $1\Omega ,0.1\Omega \text{ and 0}\text{.011}\Omega $ respectively.

Note:
In solving problems like these, we should understand the multiple connections correctly. Error in any one connection could render our complete solution wrong. Also, while performing lengthy calculations, one should be careful at each step of the process.