Question

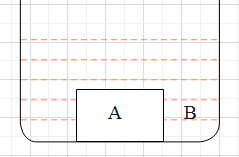
A parallel sided block of a glass of refractive index 1.5 which is 36 mm thick rests on the floor of a tank which is filled with water (refractive index = 4/3). The difference between the apparent depth of the floor at A & B when seen from vertically above is equal to:

A. 2 mm
B. 3 mm
C. 4 mm
D. none of these

Answer 1

Hint: Using the formula for calculating the apparent depth, the calculation should be carried out. The apparent depth of the floors A and B should be calculated using the apparent depth formula. Then, the difference between the apparent depths of the floor should be calculated.

Formula used:
 \[A=\dfrac{{{t}_{1}}}{{{\mu }_{1}}}+\dfrac{{{t}_{2}}}{{{\mu }_{2}}}\]

Complete step by step answer:
From given, we have the data,
The refractive index of a parallel sided block of glass, \[{{\mu }_{2}}=1.5\]
The thickness of the parallel sided block of glass, \[{{t}_{2}}=36\,mm\]
The refractive index of the water filled in the tank, \[{{\mu }_{1}}=\dfrac{4}{3}\]
Let the thickness of the tank filled with water be \[{{t}_{1}}=d\],
We will make use of the formula for calculating the apparent depth, given by,
\[A=\dfrac{{{t}_{1}}}{{{\mu }_{1}}}+\dfrac{{{t}_{2}}}{{{\mu }_{2}}}\]
Where \[{{t}_{1}},{{t}_{2}}\] are the thickness of the materials and \[{{\mu }_{1}},{{\mu }_{2}}\] are refractive indexes.
Firstly, compute the apparent depth in the case floor A.
Here the refractive indices are: \[{{\mu }_{1}}={}^{4}/{}_{3},{{\mu }_{2}}=1.5\]
So, we have,
\[A=\dfrac{d}{{}^{4}/{}_{3}}+\dfrac{36}{1.5}\] …… (1)

Secondly, compute the apparent depth in the case floor B.
Here the refractive indices are: \[{{\mu }_{1}}={}^{4}/{}_{3}={{\mu }_{2}}\]
So, we have,
\[B=\dfrac{d}{{}^{4}/{}_{3}}+\dfrac{36}{{}^{4}/{}_{3}}\]…… (2)
Now subtract the equations (1) and (2) to obtain the value of the difference in the apparent depths.
So, we get,
\[\begin{align}
  & B-A=\dfrac{36}{{}^{4}/{}_{3}}-\dfrac{36}{1.5} \\
 & \Rightarrow B-A=27-24 \\
 & \Rightarrow B-A=3\,mm \\
\end{align}\]
The difference between the apparent depth of floor at A & B when seen from vertically above is equal to 3 mm.

As the difference between the apparent depth of the floor at A & B when seen from vertically above is equal to 3 mm, thus, option (B) is correct.

Note:
The things to be on your finger-tips for further information on solving these types of problems are: The units of the given parameters should be taken into consideration while solving the problem. If in question, asked to determine the final value in mm unit, then write the final answer in terms of that unit only, even if while calculating, if you make use of other length units.