
A particle is moving with constant speed v on a circular path of r radius when it has moved by an angle of
Answer
398.7k+ views
1 likes
Hint:In order to solve this question, we will first draw the diagram to represent motion of the particle and then using the geometry of the circle we will solve for displacement, average velocity and average acceleration of the particle.
Complete step by step answer:
Let us draw the diagram in which OA and OB represent the radius r of the circular path followed by the particle and
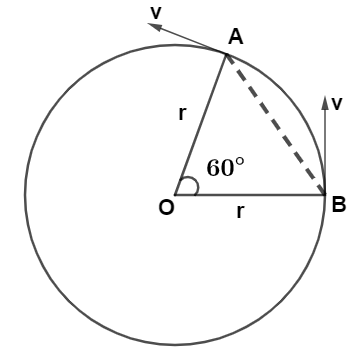
Now, In triangle OAB we see that
So, we can write
triangle OAB is a equilateral triangle because all angles are equal of
(i) Hence, the displacement of the particle AB is equal to the radius of the circular path r.
Now, Let ‘T’ be the time period of circular path which is written as
Now, in order to cover an angle of
Now, average velocity is the ratio of displacement and time taken so,
(ii) Hence, the average velocity of the particle is
Now, since the velocity of the particle is unchanged while going from Point B to point A and velocity of the particle is v and time is
(iii) Hence, the average acceleration of the particle is
Note:It should be remembered that, here the asked displacement doesn’t mention about linear and angular because when a particle moves in circular orbit, particle also cover angular displacement here arc length of AB represents the angular displacement and calculated length of line AB is simply the linear displacement of the particle.
Complete step by step answer:
Let us draw the diagram in which OA and OB represent the radius r of the circular path followed by the particle and

Now, In triangle OAB we see that
So, we can write
triangle OAB is a equilateral triangle because all angles are equal of
(i) Hence, the displacement of the particle AB is equal to the radius of the circular path r.
Now, Let ‘T’ be the time period of circular path which is written as
Now, in order to cover an angle of
Now, average velocity is the ratio of displacement and time taken so,
(ii) Hence, the average velocity of the particle is
Now, since the velocity of the particle is unchanged while going from Point B to point A and velocity of the particle is v and time is
(iii) Hence, the average acceleration of the particle is
Note:It should be remembered that, here the asked displacement doesn’t mention about linear and angular because when a particle moves in circular orbit, particle also cover angular displacement here arc length of AB represents the angular displacement and calculated length of line AB is simply the linear displacement of the particle.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




