Question

A particle is projected from point G such that it touches the points B, C, D and E of a regular hexagon of side ‘a’. Its horizontal range GH is

A. $\sqrt 3 a$
B. $\sqrt 5 a$
C. $\sqrt {7a} $
D. None

Answer 1

Hint: Find the coordinates of the points B, C, D and E and put it in the equation of the parabolic path of the projectile described by the particle. The coordinates of the points B, C, D and E satisfy the equation of the parabola.

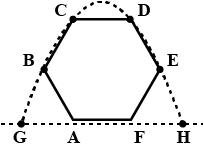
Complete step by step answer:Let origin be the midpoint of AF. Then the coordinates of B, C, D and E is given by$B\left( { - a,a\dfrac{{\sqrt 3 }}{2}} \right)$ , $C\left( {\dfrac{{ - a}}{2},a\sqrt 3 } \right)$ , $D\left( {\dfrac{a}{2},a\sqrt 3 } \right)$ , $E\left( {a,a\dfrac{{\sqrt 3 }}{2}} \right)$
The projectile will describe a parabola which is symmetrical about the y-axis. Lets the roots of the path traced by the parabola be r and –r. Then the equation of the parabola is given by $y = k(x - r)(x + r)$ \[ \Rightarrow y = k({x^2} - {r^2})\]
Since the points B and C lie on this parabola, so its coordinates must satisfy the equation of the parabola. Putting the corresponding values of x and y of B in\[y = k({x^2} - {r^2})\], we get
\[a\dfrac{{\sqrt 3 }}{2} = k({a^2} - {r^2})\] ………….(1)
Now, putting corresponding values of x and y of C in\[y = k({x^2} - {r^2})\], we get
\[a\sqrt 3 = k(\dfrac{{{a^2}}}{4} - {r^2})\] ………….(2)
Dividing equations (1) and (2), we get
\[\dfrac{1}{2} = 4\left( {\dfrac{{{a^2} - {r^2}}}{{{a^2} - 4{r^2}}}} \right)\] \[ \Rightarrow {a^2} - 4{r^2} = 8{a^2} - 8{r^2}\]
\[ \Rightarrow 7{a^2} = 4{r^2}\] \[ \Rightarrow r = \dfrac{{a\sqrt 7 }}{2}\]
As the horizontal range is from –r to r, that is 2r.
So, the horizontal range is equal to \[2 \times a\sqrt 7 = \sqrt 7 a\]
Hence, the correct option is (C).

Note:Projectile is the name given to a body thrown with some initial velocity with the horizontal direction and then allowed to move in two dimensions under the influence of gravity. The path followed by a projectile is called its trajectory. The path of a projectile projected horizontally from a point on the ground is a parabola which is symmetrical about the y-axis.