Question

A particle is projected up an inclined plane with initial speed $v = 20m/s$ at an angle = ${30^ \circ }$ with the plane. The component of its velocity perpendicular to plane when it strikes the plane is
a. $40\sqrt 3 m/s$
b. $10m/s$
c. $5\sqrt 3 m/s$
d. Data is insufficient.

Answer 1

Hint: To solve the given question consider the initial speed and the angle of the plane. We can substitute these values in the equation component’s velocity that is perpendicular to the plane.

Complete step by step answer:
We can use a diagram for our better understanding.

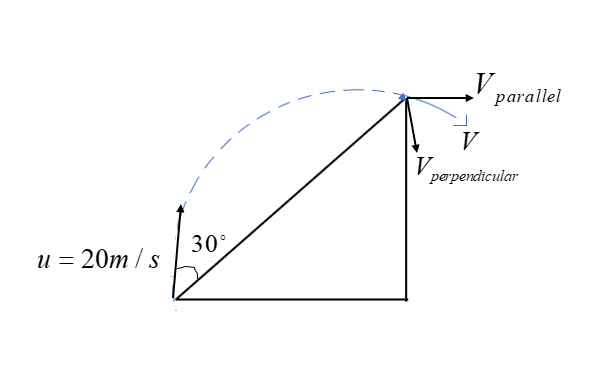
Consider the given diagram. In the question it is given that a plane is inclined at an angle of ${30^ \circ }$ and it has an initial speed of $v = 20m/s$. The blue colour line represents the projectile motion of the plane and $V$ is a component that can be written as ${V_{\text{parallel}}}$ and ${V_{\text{perpendicular}}}$.
Now let us consider the components of $V$,${V_{\text{parallel}}}$and ${V_{\text{perpendicular}}}$.

We consider the component $V$ to have the direction of $x$ and $y$.
The velocity of the component can be differentiated into two types. That is a velocity of an object at a starting or initial stage known as Initial velocity. The velocity of an object at the end stage known as the Final velocity of the object.

Consider the direction $x$ and $y$. The components along the direction of $x$ are given as $u\cos {30^ \circ }$. The direction $x$ represents the parallel component. We can write as,
$ \Rightarrow {u_x} = u\cos {30^ \circ }$ ----(1)
The component along the direction of y is given as $v\sin {30^ \circ }$. The direction $y$ represents the perpendicular component. We can write as,
$ \Rightarrow {v_y} = v\sin {30^ \circ }$ ----(2)
In the question they have asked us to find the value of the perpendicular component alone. Therefore, we can consider the perpendicular component alone.

As mentioned, there are two velocities that are initial and final velocities. Both the velocities are equal and same. So we can relate and equate the equations 1 and 2. We get,
$ \Rightarrow {v_y} = u\sin {30^ \circ }$
We know the value of the initial speed that is $v = 20m/s$ we can substitute this value in the equation. We also the value of $\sin {30^ \circ }$.We get,
$ \Rightarrow {v_y} = 20 \times \sin \dfrac{1}{2}$
Use multiplication to simplify the equation. We get,
$ \Rightarrow {v_y} = 10m/s$
$\therefore {v_y} = 10m/s$

Hence, the correct answer is option (B).

Note: The initial velocity can be calculated with the values of time, acceleration, distance and final velocity. For example, if time, acceleration final velocity is given we can write the formula as,
$u = v - at$. Where $u$ is the initial velocity, $v$ is final velocity, $a$ acceleration and $t$ is time.