
A particle is released on a vertical smooth semicircular track from point X, so that OX makes an angle,
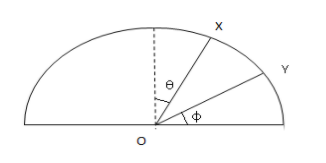
A.
B.
C.
D.

Answer
481.5k+ views
Hint: Find the distance the particle travels when it falls from point X to point Y. Use work-energy theorem to find the energy of the particle when it falls. Check for all the forces acting on the particle at point Y.
Complete Step by step answer: Let R be the radius of the semicircle and h be the distance between point X and point Y
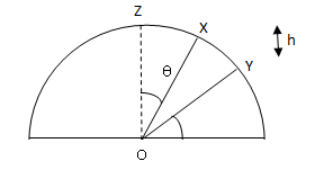
The component of OX along OZ is
Therefore, the distance travelled by the particle when it is released from X to Y is
Now, due to work done by gravity when the particle falls, it gains a velocity. Let
Work done by gravity
Where
Substituting the value of
Now, we draw a free body diagram, showing all the forces acting on the particle
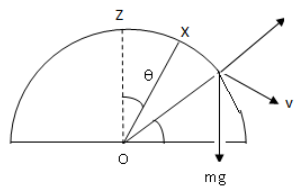
At point Y, we have along radial direction in circular motion ( in frame of particle)
Where
Given, the normal reaction vanishes,
Therefore, equation (i) becomes,
Putting the value of
Therefore, the correct answer is option (C)
Note: In this problem no other external forces were acting on the particle, so the problem was quite simple. But if there are other forces like external force or frictional forces acting on the particle then we should consider those forces in calculations too.
Complete Step by step answer: Let R be the radius of the semicircle and h be the distance between point X and point Y

The component of OX along OZ is
Therefore, the distance travelled by the particle when it is released from X to Y is
Now, due to work done by gravity when the particle falls, it gains a velocity. Let
Work done by gravity
Where
Substituting the value of
Now, we draw a free body diagram, showing all the forces acting on the particle

At point Y, we have along radial direction in circular motion ( in frame of particle)
Where
Given, the normal reaction vanishes,
Therefore, equation (i) becomes,
Putting the value of
Therefore, the correct answer is option (C)
Note: In this problem no other external forces were acting on the particle, so the problem was quite simple. But if there are other forces like external force or frictional forces acting on the particle then we should consider those forces in calculations too.
Latest Vedantu courses for you
Grade 9 | CBSE | SCHOOL | English
Vedantu 9 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




