Question

A particle is undergoing a horizontal circle of radius $r$ on the smooth surface of an inverted cone as mentioned in the diagram. The height of the plane of the circle above vertex be $h$. What will be the speed of the particle?

$\begin{align}
  & A.\sqrt{rg} \\
 & B.\sqrt{2rg} \\
 & C.\sqrt{gh} \\
 & D.\sqrt{2gh} \\
\end{align}$

Answer 1

Hint: First of all resolve the normal force acting there into sine and cosine components. The cosine component will be equivalent to the weight of the body and the sine component will be equivalent to the centripetal force occurring. Divide both of these and also find the tangent of the angle mentioned. These two will be equal. From this derive the equation for the speed of the particle. This will help you in answering this question.

Complete step by step answer:

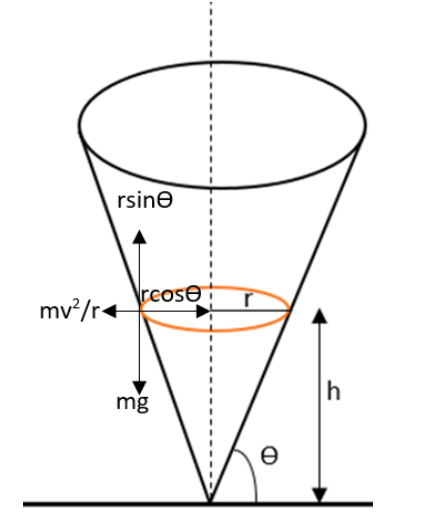
The cosine component of the normal force will be equal to the weight of the body. That is,
$N\cos \theta =mg$
The sine component of the normal force will be equal to the centripetal acceleration. That is,
$N\sin \theta =\dfrac{m{{v}^{2}}}{r}$
Let us divide both these equations which will be giving the tangent of the angle. That is,
$\tan \theta =\dfrac{{{v}^{2}}}{rg}$
From the figure we can find the tangent of the angle as,
$\tan \theta =\dfrac{h}{r}$
Comparing both these equations together can be shown as,
$\begin{align}
  & \dfrac{{{v}^{2}}}{rg}=\dfrac{h}{r} \\
 & \therefore v=\sqrt{hg} \\
\end{align}$

So, the correct answer is “Option C”.

Note: Centripetal force is a force which will be acting when a body undergoes a circular motion. The direction of the motion will be always perpendicular to the particle. This force will be directed towards the centre position of the path taken. The centripetal acceleration is the acceleration appearing for the particle when the body is having a centripetal force in action. This acceleration will also be directed towards the centre.