Question

A particle on a stretched string supporting a travelling wave, takes minimum time $5\;ms$ to move from its mean position back to the mean position. The distance between two consecutive particles, which are at their mean position, is $2\;cm$. Find the frequency, wavelength and wave speed.

Answer 1

Hint: Try to understand that the wave is produced by particles vibrating about their mean positions. Remember that the time period defines the amount of time the particle takes to execute one vibration(cycle) and is inversely proportional to the frequency of vibration. Intuitively recall the relation that relates frequency and wavelength to the wave speed by looking at the units they are expressed in.

Formula used:
Time taken for a particle to move from mean position back to mean position = $\dfrac{T}{2}$, T is the Time period of vibration of particle on the stretched string.
Frequency of vibration $f = \dfrac{1}{T}$
Wave speed $v = \dfrac{\lambda}{T} = \lambda \; f$, where $\lambda$ is the wavelength.

Complete step by step answer:
We have a particle vibrating on a stretched string. Such a vibration carries a wave. This is a case of simple harmonic motion.

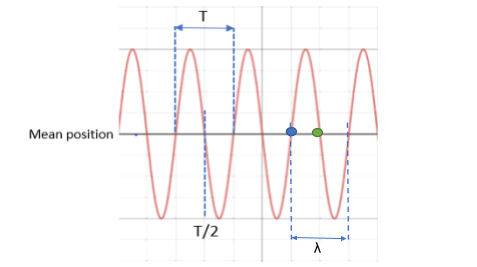
If we take T to be the total time period of vibration, the vibrating particle reaches the mean position back at $\dfrac{T}{2}$, while it reaches its extreme position at $\dfrac{T}{4}$.
The question says that the particle takes $5\;ms$ or $5 \times 10^{-3}\;s$ to move between its consecutive mean positions i.e.,
$\dfrac{T}{2} = 5\;ms \Rightarrow T = 5 \times 2 = 10\;ms$
a)Therefore, our frequency of vibration f is found to be:
$f = \dfrac{1}{T} = \dfrac{1}{10 \times 10^{-3}} = \dfrac{1}{10^{-2}} \Rightarrow f = 100\; Hz$
b)The distance between two particles is given as $2\;cm$. The particles on a string always vibrate to and from consecutive mean positions from each other.
With the help of the diagram, we can deduce that the wavelength of the wave produced as a result of these vibrations is two times the distance between consecutive vibrating particles i.e.,
Wavelength $\lambda = 2 \times$ distance between the two particles $= 2 \times 2 = 4\;cm$
c)The wave speed can be expressed in terms of wavelength and wave frequency as follows:
Wave Speed $v = f \times \lambda = 100 \times 4 = 400 cm\;s^{-1} \Rightarrow v = 4 ms^{-1}$

Note:
Sometimes the question is tweaked by providing the time taken for the particle to vibrate from the mean to the extreme position. In that case, remember that the vibrating particle will take $\dfrac{T}{4}$ to move to the extreme position. Also remember that the particles on the stretched string produce travelling waves that are the consequence of the particles vibrating about their mean position, and every mean position is located at half the wavelength of the wave produced in case of simple harmonic motion.