Question

A path of width 3.5m runs around a semi-circular grassy plot whose perimeter is 72m. Find the area of the path. \[\left( {{\text{Use }}\pi = \dfrac{{22}}{7}} \right)\]

Answer 1

Hint: Let us first draw the figure of plot and the path. And the find the area of semicircle included path and area of semicircle excluded path (plot only).

Complete step-by-step answer:

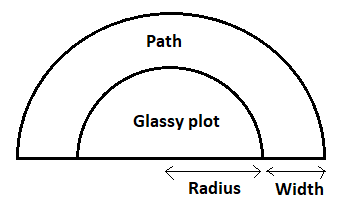
As we know that the perimeter of the semicircle is calculated as \[\pi r\] + diameter = \[\pi r + 2r\]. Where r is the radius of semicircle.
So, let the radius of the grassy plot be r metres.

And it is given that the perimeter of the grassy plot is 72m.
\[
  \pi r + 2r = 72 \\
  r\left( {\pi + 2} \right) = 72 \\
  r\left( {\dfrac{{22}}{7} + 2} \right) = 72 \\
\]
Now taking LCM on the LHS of the above equation. We get,
\[r\left( {\dfrac{{22 + 14}}{7}} \right) = \dfrac{{36r}}{7} = 72\]

Now multiplying both sides of the above equation by \[\dfrac{7}{{36}}\]. We get,
\[r = 72 \times \dfrac{7}{{36}} = 14\]metres.
Now as we can see from the above figure that the radius of outer semicircle (plot included with path) is the sum of radius of inner semicircle and width of the path.
So, let the radius of outer semicircle be R metres.
So, R = r + width of the plot = 14 m + 3.5 m = 17.5 metres
Now we are asked to find the area of the path.
And as we can see from the above figure that the area of the path is the area of the inner semicircle (glassy plot) subtracted from the area of the outer semicircle (glassy plot with path included).
As we know that the area of the semicircle with radius r is \[\dfrac{{\pi {r^2}}}{2}\].
So, the area of the outer semicircle (glassy plot with path included) will be equal to \[\dfrac{{\pi {R^2}}}{2} = \dfrac{{\pi {{\left( {17.5} \right)}^2}}}{2} = 153.125\pi {\text{ }}{m^2}\]
And the area of the inner semicircle (glassy plot) will be equal to \[\dfrac{{\pi {r^2}}}{2} = \dfrac{{\pi {{\left( {14} \right)}^2}}}{2} = 98\pi {\text{ }}{m^2}\]
So, the area of the path will be = area of outer semicircle – area of the inner semicircle = \[153.125\pi - 98\pi = 55.125\pi = 55.125 \times \dfrac{{22}}{7} = 173.25{\text{ }}{m^2}\]
Hence, the area of the path will be \[173.25{\text{ }}{m^2}\].
Note:- Whenever we come up with this type of problem then first, we have to draw the figure. And then we had to calculate the radius of the inner semicircle by comparing the given perimeter with \[\pi r + 2r\] and after that we will find the radius of outer semicircle by adding the width of the road to the radius of inner semicircle. And at last to calculate the area of the path we should first find the area of inner and outer semicircle using the formula of the area of the semicircle i.e. \[\dfrac{{\pi {r^2}}}{2}\]. And then subtract the area of inner semicircle from the area of outer semicircle to get the required area of the path.