Question

A peacock on a pillar of 9 feet height on seeing a snake coming towards its hole situated just below the pillar from a distance of 27 feet away from the pillar will fly to catch it. If both possess the same speed, how far from the pillar are they going to meet?

Answer 1

Hint: Firstly we have to draw a diagram. Then we have to assume the distance when the peacock and snake will meet. We have to use Pythagoras theorem then we have to evaluate the question accordingly to get the assumed value of this problem.

Complete step by step solution:
First of all make a diagram so that we can understand the position of the peacock and the snake place.

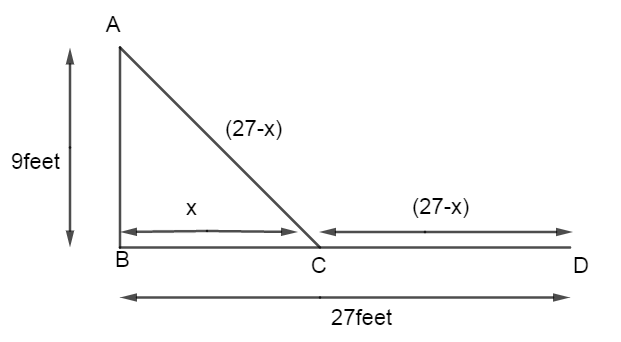
Let us assume that the peacock and snake meet at x feet from the pillar as shown in the above figure. Let BC=x feet. It is given in the question that the peacock is on a pillar of 9 feet height, therefore AB=9 feet.
And according to the question the snake is coming towards the peacock's hole situated just below the pillar from a distance of 27 feet away from the pillar. So the given distance is BD=27 feet
In the question we know the snake is coming towards its hole situated just below the pillar. And we know that the distance from snake to pillar is BD=27. We assume that the peacock and snake meet at x feet from the pillar. The peacock moved the same distance the snake moved. So \[AC=CD=\left( 27-x \right)\]
In the \[\Delta ABC\] where \[\angle B={{90}^{\circ }}\] and BC is the base AB is the height and AC is the hypotenuse of the triangle now we can use Pythagoras theorem, where \[bas{{e}^{2}}+heigh{{t}^{2}}=\text{hypotenuse}{{\text{e}}^{2}}\]
Now according to the formulae,
\[\begin{align}
  & A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} \\
 & \Rightarrow {{\left( 27-x \right)}^{2}}={{9}^{2}}+{{x}^{2}} \\
\end{align}\]
Using \[{{\left( a-b \right)}^{2}}={{a}^{2}}-2\times a\times b+{{b}^{2}}\] we get,
\[\Rightarrow {{27}^{2}}-2\times 27\times x+{{x}^{2}}=81+{{x}^{2}}\]
Removing \[{{x}^{2}}\] from both side,
\[\begin{align}
  & \Rightarrow 729-54x-81=0 \\
 & \Rightarrow 54x-648=0 \\
 & \Rightarrow 54x=648 \\
 & \Rightarrow x=\dfrac{648}{54} \\
 & \Rightarrow x=12 \\
\end{align}\]

Hence, the peacock and snake are going to meet at a distance of 12 feet from the pillar.

Note: In this problem the diagram is key to understand the question properly. Some students can’t draw the question, this question is hard to solve without a diagram. They also have to know the Pythagoras theorem to evaluate the problem further. They have to remember and carefully evaluate \[{{\left( a-b \right)}^{2}}={{a}^{2}}-2\times a\times b+{{b}^{2}}\] this formulae.