Question

A person $1.65m$ tall casts $1.5m$ shadow. At the same time, a lamp posts casts a shadow of $5.4m$.Find the height of lamp post

Answer 1

Hint: Approach the solution by drawing the diagrams of a person and lamp posts with given data to know which concept is used.
Here a person is of $1.65m$ tall and cast shadow of $1.5m$
And also shadow of lamp post =$5.4m$
We know that the angle is the same as the incident that occurred at the same point in time.
So, here sum makes the same angle of hitting the top of the person and top of the lamppost.

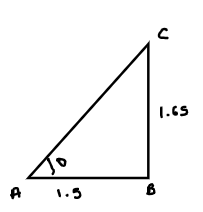
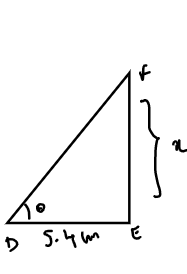
Therefore they are similar triangles $\Delta ABC\& \Delta DEF$
So, as they are the same triangles then $ \Rightarrow \frac{{AB}}{{DE}} = \frac{{CB}}{{EF}}$their radius of side is also the same.
That means

 $ \Rightarrow \frac{{AB}}{{DE}} = \frac{{CB}}{{EF}}$
Here let $EF = xcm$
$
   \Rightarrow \frac{{1.5}}{{5.4}} = \frac{{1.65}}{x} \\
   \Rightarrow x = \frac{{1.65 \times 5.4}}{{1.5}} \\
   \Rightarrow x = 5.94m \\
 $
Therefore height of lamppost=$5.94m$

NOTE: In this type problems plotting the diagram with proper position gives the correct answer.Here we know that the angle is the same as the incident that occurred at the same point in time. So by using this condition on two diagrams we have equated the value and on further simplification we get the answer.