Question

A person is in between two vertical mountains. The person fires a gun then hears a first echo from the nearby mountain in a time 3 s and hears a second echo from the far mountain in a time 4 s. The person hears the third echo after
A. 5s
B. 6s
C. 7s
D. 8s

Answer 1

Hint: When the person fires a gun, he hears the first echo from the nearby mountain and the second echo from the far mountain. The third echo will be heard by the sound which is first reflected from the nearby mountain and then reflected from the far mountain. Use the relation between distance, velocity and time to determine the time for each echo.

Formula used:
\[d = v\,t\]
Here, \[d\] is the distance, \[v\] is the velocity and \[t\] is the time.

Complete step by step answer:
The following figure represents the distance between two mountains and a person standing between the two mountains.

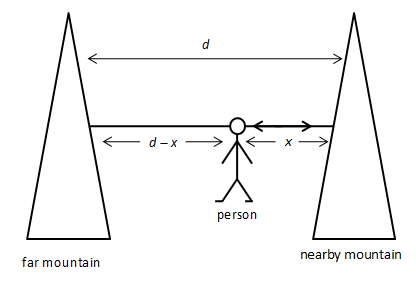
In the above figure, \[d\] is the distance between the two mountains and\[x\] is the distance between the person and the nearby mountain.

When the person fires a gun, he hears the first echo from the nearby mountain and the second echo from the far mountain. The third echo will be heard by the sound which is first reflected from the nearby mountain and then reflected from the far mountain.

From the above figure, the first echo of sound travels a distance 2x. The second echo of sound travels a distance \[2\left( {d - x} \right)\]. The third echo of sound will travel a distance \[2x + 2\left( {d - x} \right)\] as obvious.


We have the relation between distance, velocity, and time as follows,
\[d = v\,t\]

The distance travelled by the first echo is,
\[2x = v\,{t_1}\]

Here, \[v\] is the velocity of sound and \[\,{t_1}\] is the time of the first echo.

Substitute 3 s for \[\,{t_1}\] in the above equation.
\[2x = v\,\left( 3 \right)\]
\[ \Rightarrow 2x = 3v\] ...... (1)

The distance travelled by the second echo is,
\[2\left( {d - x} \right) = v\,{t_2}\]
\[ \Rightarrow 2d - 2x = v\,{t_2}\] ...... (2)

Here, \[{t_2}\] is the time for the second echo.

Substitute \[3v\] for \[2x\]and 4 s for \[{t_2}\] in the above equation.
\[2d - 3v = v\,\left( 4 \right)\]
\[ \Rightarrow 2d - 3v = 4v\]
\[ \Rightarrow 2d = 7v\]
\[ \Rightarrow \dfrac{{2d}}{v} = 7\] ...... (3)

The distance travelled by the third echo is,
\[2x + 2\left( {d - x} \right) = v\,{t_3}\]

Here, \[\,{t_3}\] is the time for the third echo.

Solve the above equation further as follows,
\[2x + 2d - 2x = v\,{t_3}\]
\[ \Rightarrow 2d = v\,{t_3}\]
\[ \Rightarrow {t_3} = \dfrac{{2d}}{v}\]

From equation (3), substitute 7 for \[\dfrac{{2d}}{v}\] in the above equation.
\[{t_3} = 7\,s\]

Therefore, the third echo will be heard after 7 seconds.

So, the correct answer is option (C).

Note:
For an echo, the sound fired by the gun travels twice a distance between the person and the mountain and not the distance between the person and the mountain. While solving such types of questions where the distance between the two reflecting objects of sound is not given, you should first find the distance between the source and nearby object and then the time required for the second echo. These two equations will eventually give you the time for the third echo.